Relativität der Gleichzeitigkeit

Man braucht somit nicht nur eine klare Definition der Gleichzeitigkeit von Ereignissen, sondern auch ein Messverfahren, wie man Gleichzeitigkeit feststellen kann.

Wie kann man Gleichzeitigkeit definieren?

Ob zwei räumlich getrennte Ereignisse gleichzeitig erfolgen oder nicht, ist davon abhängig, wie man den Begriff der Gleichzeitigkeit definiert. ALBERT EINSTEIN (1879-1955) hat dazu in seiner speziellen Relativitätstheorie nicht nur eine klare Definition, sondern zugleich auch ein Messverfahren angegeben.
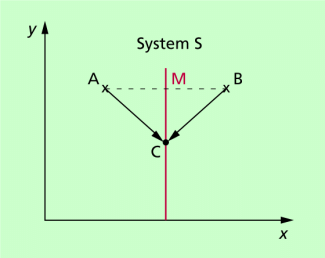
Als Beispiel betrachten wir ein Inertialsystem S und zwei verschiedene Orte A und B, in dem Ereignisse vor sich gehen (Bild 2). Ein solches Ereignis kann z.B. der Start einer Uhr, das Auslösen eines Steuermechanismus, das Aussenden eines Signals oder eine Explosion sein. Im Punkt C des gleichen Inertialsystems soll sich ein Beobachter befinden. Wann registriert er die Ereignisse, die in A und B stattfinden, als gleichzeitig?
Ausgangspunkt für die Definition der Gleichzeitigkeit ist die Konstanz der Vakuumlichtgeschwindigkeit. Nimmt man an, dass von A und B Lichtsignale ausgehen, dann legen diese Lichtsignale wegen der Konstanz der Lichtgeschwindigkeit in der gleichen Zeit den gleichen Weg zurück. Deshalb definiert man:

Zwei Ereignisse an voneinander getrennten Orten erfolgen in einem Inertialsystem dann gleichzeitig, wenn das zur Zeit der Ereignisse ausgesendete Lichtsignal sich in der Mitte ihrer Verbindungslinie trifft.

Diese Definition der Gleichzeitigkeit wird auch genutzt, um Uhren synchronisieren. Zwei Uhren werden dann gestartet, wenn Lichtsignale dort eintreffen, die zum gleich Zeitpunkt von der Mitte zwischen den beiden Uhren ausgegangen sind. Beide Uhren laufen dann synchron. Man bezeichnet diese Art der Synchronisation als EINSTEIN-Synchronisation. Weiter Erläuterungen dazu sind unter dem Stichwort „Lichtuhren“ zu finden.
Praktisch realisiert wird heute die Synchronisation von Atomuhren in folgender Weise: Eine Atomuhr, die synchronisiert werden soll, erhält von einer anderen Atomuhr ein Funksignal, dass beim Eintreffen sofort zurückgesendet wird. Aus der Konstanz der Lichtgeschwindigkeit ergibt sich der genaue Zeitpunkt des Eintreffens aus der halben Gesamtlaufzeit. Auf diese Weise können Atomuhren bis auf eine Genauigkeit von einer Nanosekunde synchronisiert werden.
Werden Signale über Kabel weitergeleitet, so muss die Laufzeit von Signalen in dem betreffenden Medium (Lichtleiter, Kupferkabel) berücksichtigt werden.

Gleichzeitigkeit ist relativ

Die obige Betrachtung bezog sich auf ein Inertialsystem S. Betrachtet man dieselben Ereignisse von einem anderen Inertialsystem S' aus, das sich gegenüber dem System S bewegt, dann erfolgen die Ereignisse in A und B nicht gleichzeitig.
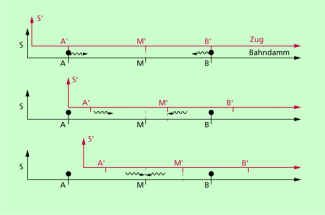
Das wird am Beispiel des folgenden Gedankenexperiment es deutlich, das auf ALBERT EINSTEIN zurückgeht: Wir betrachten die Bewegung eines sehr langen Zuges. Mit diesem Zug ist das System S' verbunden, bewegt sich also mit dem Zug mit (Bild 3). Der Zug bewegt sich längs eines geraden Bahndammes. Mit diesem Bahndamm ist das System S verbunden. Wir haben damit zwei Systeme, wobei wir annehmen, dass das System S ruht und sich S' mit der Geschwindigkeit v nach rechts bewegt. Dargestellt ist in Bild 3 der Sachverhalt aus Sicht eines Beobachters in S. Von den Punkten A und B bzw. A' und B', die zum Zeitpunkt t = 0 zusammenfallen, gehen zum gleichen Zeitpunkt Lichtsignale aus. Ihre Bewegung ist in den Skizzen in drei Phasen dargestellt.

Für einen Beobachter, der sich im System S am Punkt M befindet, ergibt sich:

• Der Lichtblitz von B erreicht den Punkt M' im System S' früher als der Lichtblitz von A (mittlere Skizze). M' wird also von beiden Lichtsignalen nicht gleichzeitig erreicht, damit auch von einem Beobachter, der sich dort befindet, nicht als gleichzeitig registriert.
• Zu einem späteren Zeitpunkt registriert der Beobachter in M beide Lichtblitze gleichzeitig.

Dieser Sachverhalt wird Relativität der Gleichzeitigkeit genannt und kann zusammenfassend folgendermaßen formuliert werden:

Zwei Ereignisse, die in einem Inertialsystem S an verschiedenen Orten gleichzeitig stattfinden, erfolgen in einem dazu bewegten Inertialsystem S' nicht gleichzeitig.

Relativität der Gleichzeitigkeit, betrachtet mithilfe der LORENTZ-Transformation
Wir gehen von dem in Bild 2 dargestellten Sachverhalt aus: Zwei Ereignisse, z.B. das Aussenden von Lichtsignalen, finden im System S in den Punkten A und B mit den Koordinaten $x_1\text{und}{x}_2$gleichzeitig statt. Das bedeutet für einen Beobachter in M, dass gilt:

$t_1=t_2\text{oder}\Delta t=t_2-t_1=0$

Mithilfe der LORENTZ-Transformation können die Werte für einen Beobachter im System S' bestimmt werden:

$\begin{array}{l}{t}_1\text{'}=k(t-\frac{v}{c^2}{x}_1)t_2\text{'}=k(t-\frac{v}{c^2}{x}_2)\\ \text{mit}k=\frac{1}{\sqrt{1-v^2/c^2}}\text{(LORENTZ-Faktor)}\\ \text{Damit erhält man für die Zeitdifferenz:}\\ \Delta t\text{'}=t_2\text{'}-t_1\text{'}\\ \Delta t\text{'}=k(t-\frac{v}{c^2}{x}_2)-k(t-\frac{v}{c^2}{x}_1)\\ \Delta t\text{'}=k\frac{v}{c^2}{x}_1-\frac{v}{c^2}{x}_2\\ \Delta t\text{'}=k\frac{v}{c^2}(x_1-x_2)\ne 0\end{array}$

Schlussfolgerung: Beide Ereignisse, die im System S gleichzeitig vor sich gehen, sind für einen Beobachter in S' nicht gleichzeitig.