Eigenschaften des Vektorprodukts

Für das Vektorprodukt gelten das Alternativgesetz und das Distributivgesetz.
Das Assoziativgesetz dagegen trifft im Allgemeinen nicht zu.
Geometrische Anwendungen sind neben der Berechnung des Flächeninhalts (von Parallelogrammen) das Bestimmen des Schnittwinkels zweier Ebenen, das Ermitteln des Normalenvektors einer Ebene oder das Berechnen des Abstands zweier windschiefer Geraden.

Unter dem Vektorprodukt $\vec{a} \times \vec{b}$ zweier Vektoren $\vec{a} u n d \vec{b}$ versteht man den im Raum durch die folgenden drei Bedingungen charakterisierten Vektor $\vec{v}$ :
Bild

Aus dieser Definition ergibt sich, dass der Betrag des Vektorprodukts zweier Vektoren gleich der Inhaltsmaßzahl des von ihnen aufgespannten Parallelogramms ist.

Deutung des Betrages des Vektorprodukts als Parallelogrammflächeninhalt

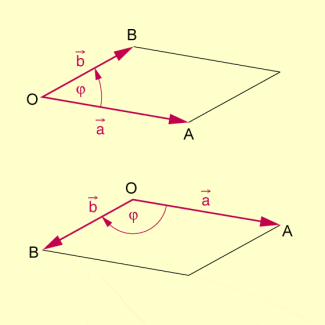
Für das Vektorprodukt gelten die folgenden Rechengesetze :

$\vec{a} \times \vec{b} = - (\vec{b} \times \vec{a})$ bzw. $\vec{a} \times \vec{b} = - \vec{b} \times \vec{a}$
(Alternativgesetz)
$(\vec{a} + \vec{b}) \times \vec{c} = \vec{a} \times \vec{c} + \vec{b} \times \vec{c}$
(Distributivgesetz)
$λ (\vec{a} \times \vec{b}) = (λ \vec{a}) \times \vec{b} = \vec{a} \times (λ \vec{b}) (λ \in ℝ)$
(Multiplikation mit einer reellen Zahl)

Anmerkung: Das Assoziativgesetz trifft im Allgemeinen nicht zu.

Aufgrund der Definition des Vektorprodukts gilt $\vec{a} \times \vec{b} = \vec{o}$ genau dann, wenn $\vec{a} u n d \vec{b}$ linear abhängig sind.

Dies korrespondiert mit der oben angegebenen Deutung des Betrags des Vektorprodukts als Inhaltsmaßzahl eines Parallelogramms: Sind $\vec{a} u n d \vec{b}$ linear abhängig, so ist $∢ (\vec{a}; \vec{b})$ gleich $0 ° o d e r 180 °$ , und das von $\vec{a} u n d \vec{b}$ aufgespannte Parallelogramm entartet zu einer Strecke.

Nun soll das Vektorprodukt von $\vec{a} u n d \vec{b}$ von für den Fall bestimmt werden, dass die beiden Vektoren durch ihre Koordinaten bezüglich eines räumlichen kartesischen Koordinatensystems gegeben sind.

Darstellung von Vektoren mithilfe von Einheitsvektoren im räumlichen kartesischen Koordinatensystem

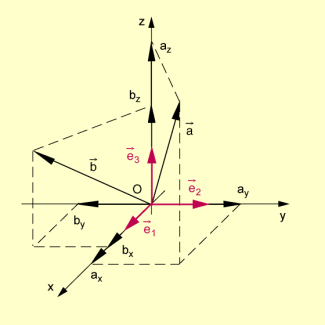
Für die in Koordinatendarstellung gegebenen Vektoren
$\vec{a} = (\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}) = a_{x} \vec{e_{1}} + a_{y} \vec{e_{2}} + a_{z} \vec{e_{3}}$ und
$\vec{b} = (\begin{matrix} b_{x} \\ b_{y} \\ b_{z} \end{matrix}) = b_{x} \vec{e_{1}} + b_{y} \vec{e_{2}} + b_{z} \vec{e_{3}}$
gilt dann:
$\vec{a} \times \vec{b} = (a_{x} \vec{e_{1}} + a_{y} \vec{e_{2}} + a_{z} \vec{e_{3}}) \times (b_{x} \vec{e_{1}} + b_{y} \vec{e_{2}} + b_{z} \vec{e_{3}})$

Unter Verwendung des Distributivgesetzes des Vektorprodukts erhält man:
$\begin{matrix} \vec{a} \times \vec{b} = a_{x} b_{x} (\vec{e_{1}} \times \vec{e_{1}}) + a_{x} b_{y} (\vec{e_{1}} \times \vec{e_{2}}) + a_{x} b_{z} (\vec{e_{1}} \times \vec{e_{3}}) \\ = a_{y} b_{x} (\vec{e_{2}} \times \vec{e_{1}}) + a_{y} b_{y} (\vec{e_{2}} \times \vec{e_{2}}) + a_{y} b_{z} (\vec{e_{2}} \times \vec{e_{3}}) \\ = a_{z} b_{x} (\vec{e_{3}} \times \vec{e_{1}}) + a_{z} b_{y} (\vec{e_{3}} \times \vec{e_{2}}) + a_{z} b_{z} (\vec{e_{3}} \times \vec{e_{3}}) \end{matrix}$

Wegen
$\begin{array}{l} \vec{e_{1}} \times \vec{e_{1}} = \vec{e_{2}} \times \vec{e_{2}} = \vec{e_{3}} \times \vec{e_{3}} = \vec{0}; \\ \vec{e_{1}} \times \vec{e_{2}} = \vec{e_{3}}; \vec{e_{2}} \times \vec{e_{3}} = \vec{e_{1}}; \vec{e_{3}} \times \vec{e_{1}} = \vec{e_{2}}; \\ \vec{e_{2}} \times \vec{e_{1}} = - \vec{e_{3}}; \vec{e_{3}} \times \vec{e_{2}} = - \vec{e_{1}}; \vec{e_{1}} \times \vec{e_{3}} = - \vec{e_{2}} \end{array}$

folgt daraus:
$\vec{a} \times \vec{b} = (a_{y} b_{z} - a_{z} b_{y}) \vec{e_{1}} + (a_{z} b_{x} - a_{x} b_{z}) \vec{e_{2}} + (a_{x} b_{y} - a_{y} b_{x}) \vec{e_{3}}$

Unter Verwendung der Matrizen- bzw. Determinantenschreibweise lässt sich dieses Ergebnis für das Vektorprodukt übersichtlich notieren.

Sind
$\vec{a} = (\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}) u n d \vec{b} = (\begin{matrix} b_{x} \\ b_{y} \\ b_{z} \end{matrix})$
zwei Vektoren im Raum, so gilt:
$\begin{array}{l} \vec{a} \times \vec{b} = | \begin{matrix} \vec{e_{1}} & \vec{e_{2}} & \vec{e_{3}} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{matrix} | \\ = (a_{y} b_{z} - a_{z} b_{y}) \vec{e_{1}} + (a_{z} b_{x} - a_{x} b_{z}) \vec{e_{2}} + (a_{x} b_{y} - a_{y} b_{x}) \vec{e_{3}} \\ = (\begin{matrix} a_{y} b_{z} - a_{z} b_{y} \\ a_{z} b_{x} - a_{x} b_{z} \\ a_{x} b_{y} - a_{y} b_{x} \end{matrix}) \end{array}$

Anmerkung: Natürlich ist die im obigen Satz verwendete Schreibweise im engeren Sinne keine Determinante, da $\vec{e_{1}}, \vec{e_{2}}, \vec{e_{3}}$ keine reellen Zahlen sind. Diese Schreibweise eignet sich hier aber zu einer übersichtlichen Darstellung.

Als geometrische Anwendungen des Vektorprodukts sind neben der genannten Flächeninhaltsberechnung beispielsweise das Bestimmen des Schnittwinkels zweier Ebenen, das Ermitteln des Normalenvektors einer Ebene oder das Berechnen des Abstands zweier windschiefer Geraden zu nennen.

Beispiel: Es ist der Normaleneinheitsvektor der Ebene mit
$ε : \vec{x} = (\begin{matrix} 2 \\ - 1 \\ 3 \end{matrix}) + r (\begin{matrix} 2 \\ 1 \\ 5 \end{matrix}) + s (\begin{matrix} - 2 \\ 3 \\ - 1 \end{matrix})$
zu ermitteln.

Wir bilden dazu das Vektorprodukt der beiden Richtungsvektoren
$\vec{a} = (\begin{matrix} 2 \\ 1 \\ 5 \end{matrix}) u n d \vec{b} = (\begin{matrix} - 2 \\ 3 \\ - 1 \end{matrix})$ von $ε$
und dividieren den so erhaltenen Vektor (der senkrecht zu $ε$ ist) durch seinen Betrag:
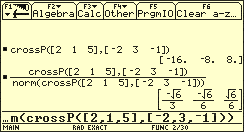
$\begin{matrix} \vec{a} \times \vec{b} = | \begin{matrix} \vec{e_{1}} & \vec{e_{2}} & \vec{e_{3}} \\ 2 & 1 & 5 \\ - 2 & 3 & - 1 \end{matrix} | = - 16 \vec{e_{1}} - 8 \vec{e_{2}} + 8 \vec{e_{3}} = (\begin{matrix} - 16 \\ - 8 \\ 8 \end{matrix}) \\ {\vec{n}}^{0} = \frac{\vec{a} \times \vec{b}}{| \vec{a} \times \vec{b} |} = \frac{1}{\sqrt{384}} (\begin{matrix} - 16 \\ - 8 \\ 8 \end{matrix}) = \frac{1}{6} \sqrt{6} (\begin{matrix} - 2 \\ - 1 \\ 1 \end{matrix}) \end{matrix}$

Verwendet man zur Berechnung von ${\vec{n}}^{0}$ einen Grafiktaschenrechner mit Computeralgebrasystem, so erhält man mit den Funktionen crossP (für Vektorprodukt) und norm (für Betrag) das in der folgenden Abbildung wiedergegebene Ergebnis. Dabei könnte noch auf das Ausweisen des Zwischenschritts in Zeile 1 verzichtet werden.

Schirmbild zum Beispiel der Ermittlung des Einheitsnormalenvektors einer Ebene

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Eigenschaften des Vektorprodukts

Rechtliches

Einloggen