Nullstellen trigonometrischer Funktionen

Viele periodische Vorgänge lassen sich durch Funktionen der Form f ( x ) = a ⋅ sin ( b ⋅ ( x − c ) ) beschreiben. Deren Graphen entstehen aus dem Graphen der Sinusfunktion durch Streckung (Stauchung) in Richtung der Koordinatenachsen und Verschiebung in Richtung der x-Achse, woraus sich Schlussfolgerungen für die Nullstellen ziehen lassen.
Für mit anderen Funktionen verkettete Sinus- und Kosinusfunktionen führt das Bestimmen der Nullstellen auf das Lösen goniometrischer Gleichungen.

Die Sinusfunktion f ( x ) = sin x       ( m i t       x ∈ ℝ ) besitzt Nullstellen für alle x ∈ { k ⋅ π ,       k ∈ ℤ } .
Der Graph der Kosinusfunktion f ( x ) = cos x       ( m i t       x ∈ ℝ ) ist gegenüber dem Graphen der Sinusfunktion um π 2 in Richtung der negativen x-Achse verschoben. Deshalb gilt für die Nullstellen von f ( x ) = cos x , dass das alle Werte x mit x ∈ { π 2 + k ⋅ π ,       k ∈ ℤ } sind.
Die Tangensfunktion f ( x ) = tan x = sin x cos x hat unendlich viele Definitionslücken, nämlich gerade die Nullstellen der Kosinusfunktion. Die Nullstellen der Tangensfunktion stimmen mit den Nullstellen der Sinusfunktion überein, d.h., sie besitzt Nullstellen für alle Werte x ∈ { k ⋅ π ,       k ∈ ℤ } .

Funktionen der Form f ( x ) = a ⋅ sin ( b ⋅ ( x − c ) )

Viele periodische Vorgänge lassen sich durch Funktionen der Form f ( x ) = a ⋅ sin ( b ⋅ ( x − c ) ) beschreiben. Im Folgenden soll untersucht werden, welchen Einfluss a, b und c auf die Nullstellen derartiger Funktionen nehmen.

Für beliebige a ,   b ,   c ∈ ℝ       m i t       a ,   b > 0 gilt für die Periode p von f ( x ) = a ⋅ sin ( b ⋅ ( x − c ) ) :
  p = 2 π b

Den Graphen einer solchen Funktion f kann man sich aus dem Graphen der Sinusfunktion schrittweise entstanden denken:

  1. Der Faktor a bewirkt eine Streckung (Stauchung) in Richtung y-Achse mit dem Faktor a, d.h., die Funktionen f ( x ) = sin x und f ( x ) = a ⋅ sin x besitzen die gleichen Nullstellen.
  2. Der Faktor b bewirkt eine Streckung (Stauchung) in Richtung x-Achse mit dem Faktor 1 b . Das hat Einfluss auf die Nullstellen von f ( x ) = sin b x , das sind alle x-Werte mit x ∈ { k ⋅ π b ,       k ∈ ℤ } .
  3. Der Summand c bewirkt eine Verschiebung in Richtung x-Achse um c Einheiten, damit verschieben sich auch die Nullstellen um c.
Graph zur Funktion des Beispiels 1 (allgemeine Sinusfunktion)

Graph zur Funktion des Beispiels 1 (allgemeine Sinusfunktion)

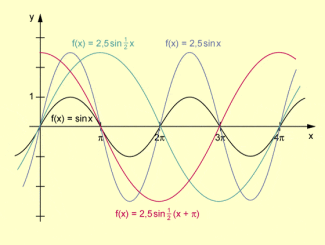
  • Beispiel 1: Es sind die Nullstellen der Funktion f(x) = 2 ,5 ⋅ sin ( 1 2 ( x + π ) ) zu bestimmen.

Der Graph der Funktion f geht aus dem Graphen der Sinusfunktion hervor durch Streckung in Richtung der y-Achse mit dem Faktor 2,5, Streckung in Richtung der x-Achse mit dem Faktor 2 sowie eine Verschiebung in Richtung der x-Achse um π Einheiten nach links.
Man überlegt sich:

  1. Die Periode von f ist p = 4 π .
  2. Nullstellen nach Streckung in Richtung der y-Achse:
    x ∈ { x   |       x = k ⋅ π ,       k ∈ ℤ }
  3. Nullstellen nach Streckung in Richtung der x-Achse:
    x ∈ { x   |     x = 2 k ⋅ π ,       k ∈ ℤ }
  4. Nullstellen nach Verschiebung in Richtung der x-Achse:
    x ∈ { x   |     x = ( 2 k − 1 ) ⋅ π ,       k ∈ ℤ }

Nullstellen im Intervall [ 0 ;   4 π ] sind dann x 1 = π  und  x 2 = 3 π .

Verkettung trigonometrischer Funktionen mit anderen Funktionen
Häufig werden Sinus- und Kosinusfunktionen mit anderen Funktionen verkettet und verknüpft. Dann sind bei der Nullstellenbestimmung goniometrische Gleichungen (trigonometrische Gleichungen) zu lösen. Im Folgenden werden dazu einige Beispiele betrachtet.

Graph zur Funktion des Beispiels 2 (verkettete Sinusfunktion)

Graph zur Funktion des Beispiels 2 (verkettete Sinusfunktion)

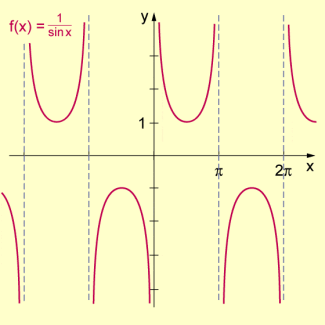
  • Beispiel 2: f ( x ) = 1 sinx

Die Funktion f hat für alle x ∈ { k ⋅ π ,       k ∈ ℤ } , und zwar für die Nullstellen der Sinusfunktion, Definitionslücken.
Nullstellen besitzt f nicht, da die Gleichung 1 sinx = 0 für kein x erfüllbar ist.
Die Funktionswerte von f sind größer gleich 1 bzw. kleiner gleich −   1 .

Graph zur Funktion des Beispiels 3 (verkettete Sinusfunktion)

Graph zur Funktion des Beispiels 3 (verkettete Sinusfunktion)

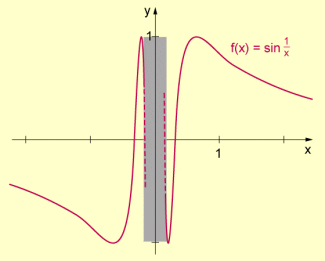
  • Beispiel 3: f(x) = sin 1 x   ( x ≠ 0)

Bestimmen der Nullstellen heißt, die Gleichung sin 1 x = 0 zu lösen. Setzt man 1 x = z , so erhält man die Gleichung sin z = 0 , die für alle z = k ⋅ π ,       k ∈ ℤ erfüllt ist. Aus x = 1 z bzw. x = 1 k ⋅ π ,       k ∈ ℤ \ { 0 } folgt, dass die Funktion die Nullstellen 1 π    und  − 1 π hat und dazwischen unendlich viele weitere Nullstellen liegen.

  • Beispiel 4: f ( x ) = 4 sin 2 x + 5 sin x − 6

Berechnen der Nullstellen im Intervall [ 0 ;   π ] führt auf die folgende goniometrische Gleichung:
  4 sin 2 x + 5 sin x − 6 = 0
Mit der Substitution sin x = z erhält man:
  4z 2 + 5z − 6 = 0   z 2 + 5 4 z − 3 2 = 0 z 1;   2 = −   5 8 ± 25 64 + 96 64 = −   5 8 ± 11 8 z 1 = 3 4 ;       z 2 = −   2
Daraus folgt sin x = 3 4 und damit x 1 ≈ 0,848 . Im Intervall [ 0 ;   π ] gibt es mit x 2 = π − x 1 ≈ 2,294 eine weitere Lösung. Die Gleichung sin x = −   2 hat keine Lösung. Damit hat f im Intervall [ 0 ;   π ] zwei Nullstellen.

Berechnung Definitionslücken Periodizität Periode Mathcad trigonometrische Gleichungen Verschiebung Sinusfunktion Streckung Tangensfunktion goniometrische Gleichungen Graphen interaktives Rechenbeispiel Kosinusfunktion
Lexikon Share
Mathe Note verbessern?
 

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

  • 40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
  • Hausaufgabenhilfe per WhatsApp
  • Original Klassenarbeiten mit Lösungen
  • Deine eigene Lern-Statistik
  • Kostenfreie Basismitgliedschaft
Mathe kostenlos lernen
Verwandte Artikel
alle anzeigen
Beliebte Artikel
alle anzeigen
Angaben zum Lexikon
Impressum
© Duden Learnattack GmbH, 2023

Einloggen