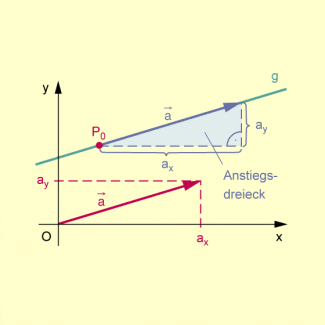
Punktrichtungsgleichung einer Geraden

Die Betrachtung eines Anwendungsbeispiels führt zur Punktrichtungsgleichung einer Geraden in der Ebene. Aus der Parameterform der Punktrichtungsgleichung einer Geraden wird anschließend eine parameterfreie Gleichung ermittelt.

Ein Auto möge auf einer geradlinigen Straße mit konstanter Geschwindigkeit $v = 108 \frac{k m}{h} = 30 \frac{m}{s}$ fahren. Dann gilt $s = t \cdot v$ , wobei s den zurückgelegten Weg und t die dazu benötigte Zeit angibt.
Unter den genannten Randbedingungen (geradlinige Straße, konstante Geschwindigkeit) kann man die Entfernung vom Ausgangspunkt der Messung zu einem Punkt $P_{1}$ berechnen, wenn das Auto für diese Strecke eine Zeit t = 20 s benötigt hat, es gilt:
$s = 20 s \cdot 30 \frac{m}{s} = 600 m$
Auf die gleiche Weise lässt sich der zurückgelegte Weg auch für jede andere Zeit t (aus dem betrachteten Zeitintervall) ermitteln. Die Zeit t übernimmt hier die Rolle eines (reellen) Parameters, während die Geschwindigkeit v eine konstante Größe ist.

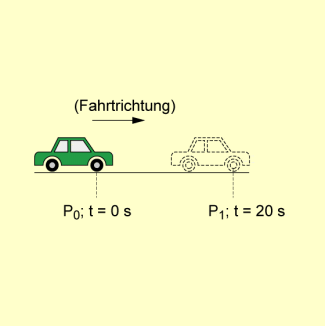
Bewegung eines Autos

Im Unterschied zur Zeit, die allein durch ihren Betrag eindeutig beschrieben ist, sind Geschwindigkeit und Weg vektorielle Größen. Wir bezeichnen sie deshalb mit $\vec{v} b z w . \vec{s}$ .
Betrachtet man nun die Straße mit dem Auto aus „genügend großer“ Entfernung, dann lässt sich die geradlinige Straße als Stück einer Geraden und das Auto als Punkt X auffassen, der sich von einem Punkt $P_{0}$ zu einem Punkt $P_{1}$ mit konstanter Geschwindigkeit bewegt.

Bewegung eines Punkts längs der x-Achse

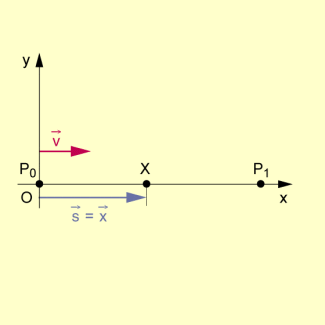
Für das Auto X kann zu jedem Zeitpunkt t (reeller Parameter) die Position auf der Geraden als Entfernung zum Punkt $P_{0}$ angegeben werden: Es gilt $\vec{s} = \vec{x} = t \vec{v}$ , wobei jetzt $\vec{x}$ die Koordinaten des Punktes X bezüglich des gewählten Koordinatensystems angibt.

Abstrahiert man nun von den konkreten Gegebenheiten und betrachtet einen Punkt $P_{0}$ und einen Vektor $\vec{a}$ in der Ebene oder im Raum, so wird dadurch diejenige Gerade g eindeutig bestimmt, die durch $P_{0}$ geht und die Richtung von $\vec{a}$ hat.

Beschreibung einer Geraden durch eine ihrer Punkte und ihre Richtung

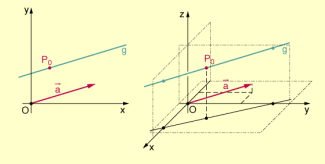
Der Vektor $\vec{a}$ heißt dementsprechend Richtungsvektor der Geraden g. Den Punkt $P_{0}$ nennt man Stützpunkt (oder auch Trägerpunkt) von g und den zugehörigen Ortsvektor ${\vec{p}}_{0}$ dann Stützvektor der Geraden g.

Der Ortsvektor $\vec{x}$ zu einem beliebigen Punkt X auf g lässt sich unter Verwendung der obigen Überlegungen durch die folgende Gleichung beschreiben:
$\vec{x} = {\vec{p}}_{0} + t \vec{a} (t \in R)$

In dieser Formel finden die Vektoraddition und die Vervielfachung eines Vektors mit einer reellen Zahl (einem Parameter) Anwendung. Zusammengefasst lässt sich feststellen:

Punktrichtungsgleichung einer Geraden (Vektorform):
Die Gerade g, die durch den Stützpunkt $P_{0}$ mit dem Ortsvektor ${\vec{p}}_{0} = \vec{O P_{0}}$ und den Richtungsvektor $\vec{a}$ ( $\vec{a} \neq \vec{o}$ ) eindeutig bestimmt ist, kann durch die Gleichung $\vec{x} = {\vec{p}}_{0} + t \vec{a} (t \in R)$ beschrieben werden.

Anmerkung: In Vektorform angegebene Gleichungen werden mitunter auch als vektorielle Gleichungen, Vektorgleichung oder als Gleichungen in Parameterform bezeichnet.

Durch die Wahl von beliebigen reellen Zahlen für den Parameter t erhält man jeweils die Beschreibung eines Punktes der Geraden g durch seine jeweiligen Koordinaten.

Ermittlung der Koordinaten von Punkten einer Geraden durch Parameterwahl

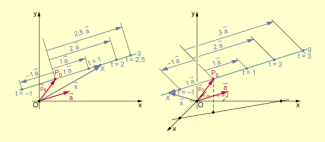
Umgekehrt lässt sich aus den Koordinaten eines beliebigen Punktes P von g der zugehörige Parameter t berechnen.

Um für eine Gerade der Ebene aus der obigen Punktrichtungsgleichung in Vektorform eine parameterfreie Gleichung (eine Gleichung in Koordinatenschreibweise ) zu erhalten, betrachten wir nun allgemein eine Gerade g, die durch einen Punkt $P_{0} (x_{0}; y_{0})$ und einen Richtungsvektor
$\vec{a} = (\begin{matrix} a_{x} \\ a_{y} \end{matrix})$
bestimmt sei.
Die Gerade g hat die Gleichung
$\vec{x} = (\begin{matrix} x_{0} \\ y_{0} \end{matrix}) + t (\begin{matrix} a_{x} \\ a_{y} \end{matrix})$ .
Wenn X(x; y) einen beliebigen Punkt von g bezeichnet, so gilt dann
$(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} x_{0} \\ y_{0} \end{matrix}) + t (\begin{matrix} a_{x} \\ a_{y} \end{matrix})$ ,
woraus sich mithilfe der Rechenregeln für Vektoren ergibt:
$(\begin{matrix} x \\ y \end{matrix}) - (\begin{matrix} x_{0} \\ y_{0} \end{matrix}) = t (\begin{matrix} a_{x} \\ a_{y} \end{matrix}), a l s o (\begin{matrix} x - x_{0} \\ y - y_{0} \end{matrix}) = (\begin{matrix} t \cdot a_{x} \\ t \cdot a_{y} \end{matrix})$ .

Durch Anwendung des Prinzips des Koordinatenvergleichs erhält man zwei Gleichungen:
$\begin{array}{l} (I) x - x_{0} = t a_{x} \\ (I I) y - y_{0} = t a_{y} \end{array}$
Löst man beispielsweise die zweite Gleichung nach t auf und setzt in die erste Gleichung ein, so erhält man nach Umformung:
$(x - x_{0}) a_{y} - (y - y_{0}) a_{x} = 0$
Hierbei handelt es sich um eine Punktrichtungsgleichung der Geraden g, die keinen Parameter t mehr enthält, die also eine parameterfreie Form dieser Geradengleichung ist.

Punktrichtungsgleichung einer Geraden in der Ebene (Koordinatenschreibweise): Die Gerade g der Ebene, die durch den Punkt $P_{0} (x_{0}; y_{0})$ und den Richtungsvektor
$\vec{a} = (\begin{matrix} a_{x} \\ a_{y} \end{matrix})$
bestimmt ist, lässt sich durch die folgende parameterfreie Gleichung beschreiben:
$(x - x_{0}) a_{y} - (y - y_{0}) a_{x} = 0$

Falls die Gerade g nicht parallel zur y-Achse verläuft, d.h., wenn $a_{x} \neq 0$ ist, nimmt diese Gleichung die Form
$y - y_{0} = \frac{a_{y}}{a_{x}} (x - x_{0}) b z w . y - y_{0} = m (x - x_{0})$ an.
Dabei ist $m = \frac{a_{y}}{a_{x}}$ der Anstieg der Geraden.

Anstiegsdreieck einer Geraden

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Punktrichtungsgleichung einer Geraden

Rechtliches

Einloggen