Trapez
Ein Viereck mit einem Paar paralleler Seiten heißt Trapez (Bild 1).
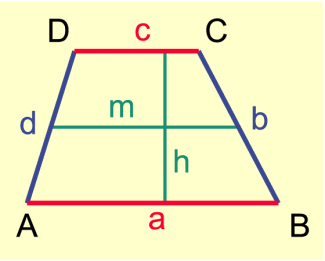
Die parallelen Seiten sind die Grundseiten, die beiden anderen Seiten die Schenkel des Trapezes.
Der Abstand der Grundseiten ist die Höhe h des Trapezes.
Die Verbindungsstrecke der Mitten der Schenkel heißt Mittellinie m.
Sind in einem Trapez die Schenkel gleich lang, so heißt es gleichschenklig. Gleichschenklige Trapeze sind achsensymmetrisch. Die Symmetrieachse ist die Mittelsenkrechte der zueinander parallelen Seiten.
Hat das Trapez einen rechten Innenwinkel, so heißt es rechtwinkliges Trapez.
Die Mittellinie m ist in jedem Trapez parallel zu den Grundseiten und halb so lang wie die Summe beider Grundseiten:
Trapez
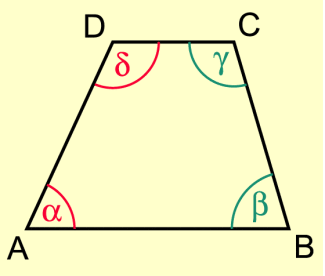
In jedem Trapez sind die an einem Schenkel anliegenden Innenwinkel entgegengesetzte Winkel an geschnittenen Parallelen. Sie ergänzen sich also zu (Bild 2):
Winkel im Trapez
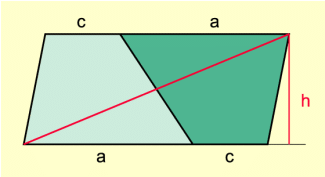
Legt man zwei kongruente (und damit flächeninhaltsgleiche) Trapeze aneinander, so besitzen sie zusammen den doppelten Flächeninhalt des Dreiecks mit der Grundseite a + c und der Höhe h (Bild 3).
Für den Flächeninhalt dieses Dreiecks und damit des Trapezes gilt:
Der Umfang des Trapez ist gleich der Summe der Längen der vier Trapezseiten:
u = a + b + c + d
Für den Umfang des gleichschenkligen Trapezes gilt:
u = a + 2b + c
Flächeninhalt eines Trapezes
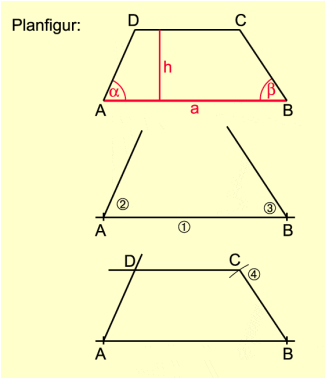
Für die Konstruktion eines Trapezes sind vier voneinander unabhängige Angaben notwendig (Bild 4).
Beispiel:
Gegeben sind die Seite a, die Höhe h sowie die Winkel .
- Auf einer Geraden wird die Strecke AB mit abgetragen.
- In A wird an die Strecke AB der Winkel angetragen.
- In B wird an die Strecke AB der Winkel angetragen.
- Zur Geraden AB wird eine Parallele im Abstand h gezeichnet. Der Schnittpunkt des freien Schenkels von mit der Parallelen ist der Punkt D. Der Schnittpunkt des freien Schenkels von mit der Parallelen ist der Punkt C.
Konstruktion eines Trapezes
Viereck Konstruktion Mittellinie interaktivrechtwinklig Trapez Mathcad Umfang Schenkel Berechnungsbeispiel Flächeninhalt gleichschenklig Höhe Rechenbeispiel
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 