Anzahl und Abmessungen von Atomen

Inzwischen kennt man nicht nur die Anzahl von Atomen in einer bestimmten Stoffmenge, sondern auch die Masse von Atomen, die Atomradien, die Kernradien und die Dichte von Atomkernen. Diese atomaren Daten können in unterschiedlicher Weise ermittelt werden. Nachfolgend sind die wichtigsten Daten zusammengestellt und erläutert, wie man die verschiedenen Größen bestimmen kann.

Anzahl von Atomen in einer bestimmten Stoffmenge bzw. Masse

Überlegungen zur Teilchenanzahl in einer bestimmten Stoffmenge gehen wesentlich auf den italienischen Physiker und Chemiker AMADEO AVOGADRO (1776-1856) zurück. Er stellte fest, dass in einer bestimmten Stoffmenge immer die gleiche Anzahl von Teilchen vorhanden ist. Erfasst wird das durch die sogenannte AVOGADRO-Konstante, die die Teilchenanzahl je Mol angibt. Es gilt:

$N_{\text{A}}=\mathrm{6,022}136\cdot {10}^{23}\frac{1}{\text{mol}}$

Für die Charakterisierung einer Stoffmenge muss die Art der Teilchen angegeben werden. Betrachtet man Atome, dann gilt:
Die Anzahl N von Atomen je Mol beträgt $\mathrm{6,022}\cdot {10}^{23}$
Für die quantitativen Zusammenhänge gelten die folgenden Beziehungen:

$\begin{array}{l}N=N_{\text{A}}\cdot nN=N_{\text{A}}\cdot \frac{m}{M}N=N_{\text{A}}\cdot \frac{V}{V_m}\\ N\text{Teilchenanzahl}\\ N_{\text{A}}\text{AVOGADRO-Konstante}\\ n\text{Stoffmenge in mol}\\ m\text{Masse der Stoffportion}\\ M\text{molare Masse des Stoffes}\\ V\text{Volumen der Stoffportion}\\ V_{\text{m}}\text{molares Volumen}\end{array}$

Kennt man die Teilchenanzahl in der bestimmten Stoffmenge, dann lässt sich mithilfe der genannten Gleichungen auch die Anzahl der Teilchen in einer bestimmten Masse berechnen. Die molare Masse kann man Tabellenwerken entnehmen. Man erhält dann:
Die Anzahl von Atomen je Gramm eines Stoffes liegt in einer Größenordnung von ${10}^{22}$Atomen.

Masse von Atomen

Die Masse von Atomen kann beispielsweise mithilfe von Massenspektrografen bestimmt werden. Genauere Informationen zum Aufbau eines solchen Spektrografen und zu den Gesetzen, die dabei eine Rolle spielen, sind unter dem Stichwort Massenspektrograf zu finden. Untersuchungen mit solchen Spektrografen haben ergeben: Die Masse von Atomen liegt zwischen ${10}^{-27}{\text{kg und 10}}^{\text{-24}}\text{kg}$.

Radius von Atomen

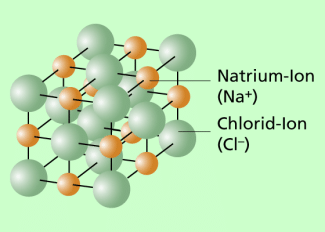
Der Atomradius bzw. der Durchmesser von Atomen kann in unterschiedlicher Weise abgeschätzt werden. Eine Möglichkeit ist der sogenannte Ölfleckversuch. Er ist unter diesem Stichwort in einem gesonderten Beitrag ausführlich beschrieben. Eine andere Möglichkeit besteht darin, von bekannten Kristallstrukturen auszugehen und durch theoretische Überlegungen zu einer Größenordnung für den Atomradius zu kommen. Wir betrachten dazu den in Bild 1 dargestellten Kochsalzkristall (NaCl), der von der chemischen Struktur her aus Natrium- und Chlorid-Ionen besteht, deren Abmessungen denen von Atomen entsprechen. Eine genauere Analyse der Struktur ergibt: Der Kristall besteht als Elementarwürfeln mit je vier Natrium- und Chloratomen. Im Unterschied zum dargestellten Modell gehen wir davon aus, dass die Atome dicht gepackt sind. Kann man die Kantenlänge eines solchen Elementarwürfels berechnen, so ergibt sich daraus eine Abschätzung für den Durchmesser eines Atoms und damit auch für den Atomradius.
Für ein Mol NaCl gilt:

$\begin{array}{l}\text{Es besteht aus}{N}_{\text{A}}=\mathrm{6,022}\cdot {10}^{23}\text{NaCl-Teilchen und damit}\\ \text{aus 2}{N}_{\text{A}}\text{Natrium- und Chloratomen}\text{.}\end{array}$

Da ein Elementarwürfel der Kantenlänge d das Volumen $\begin{array}{l}{d}^3\text{besitzt}\text{, kann man für das Volumen eines Mols}\\ \text{NaCl schreiben:}\\ V=2N_{\text{A}}\cdot d^3\text{(1)}\end{array}$

Ein Mol NaCl besitzt die molare Masse M. Geht man von der Definition der Dichte

$\begin{array}{l}\rho =\frac{M}{V}\text{aus und stellt die Gleichung nach}V\text{um}\text{,}\\ \text{dann erhält man als zweite Gleichung für das Volumen:}\\ V=\frac{M}{\rho }\text{(2)}\end{array}$

Aus den beiden Gleichungen (1) und (2) für das Volumen kann man den Atomdurchmesser abschätzen. Gleichsetzen der rechten Seiten von (1) und (2) ergibt:

$\begin{array}{l}2N_{\text{A}}\cdot d^3=\frac{M}{\rho }\\ \text{Durch Umstellen nach}d\text{erhält man:}\\ d=\sqrt[3]{\frac{M}{\rho \cdot 2N_{\text{A}}}}\\ \text{Das Einsetzen der entsprechenden Werte für Kochsalz}\\ \text{ergibt:}\\ d=\sqrt[3]{\frac{\mathrm{58,45}\text{g}\cdot {\text{cm}}^3\cdot \text{mol}}{\text{mol}\cdot \text{2}\text{,16 g}\cdot \text{2}\cdot \text{6}\text{,022}\cdot {\text{10}}^{\text{23}}}}\\ \underset{¯}{d=\mathrm{2,82}\cdot {10}^{-10}\text{cm}}\end{array}$

Wie Untersuchungen an anderen Stoffen zeigen, lässt sich dieses Ergebnis verallgemeinern und lautet dann:
Der Radius von Atomen liegt in der Größenordnung von ${10}^{-10}\text{m}$.
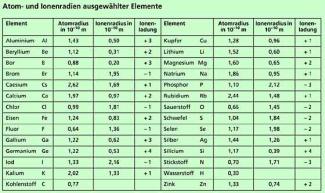
In Bild 2 sind einige Atom- und Ionenradien angegeben. Für ein Wasserstoffatom ergibt sich als Wert:
$r_{\text{B}}=\mathrm{0,529}177\cdot {10}^{-10}\text{m und damit d}\approx \text{1}\text{,06}\cdot {10}^{\text{-10}}\text{m}$
Dieser Radius wird als bohrscher Radius bezeichnet.

Der Kernradius

Für den Kernradius gilt in guter Näherung die Gleichung:
$r=\mathrm{1,3}\cdot {10}^{-15}\text{m}\cdot \sqrt[3]{A}$

Dabei ist A die Nukleonenzahl oder Massenzahl, also die Summe aus Protonenzahl und Neutronenzahl. Für ein Element mittlerer Ordnungszahl, z.B. Zinn, ergibt sich für die Massenzahl ein Wert von etwa 120 und damit für den Kernradius ein Wert von
$r=\mathrm{6,4}\cdot {10}^{-15}.$

Dichte der Kernmaterie

Die Dichte der Kernmaterie ergibt sich aus Masse und Volumen.
$\begin{array}{l}\rho =\frac{m}{V}\\ \text{Betrachtet man ein beliebiges Atom}\text{, dann ergibt sich}\\ \text{dafür:}\\ \rho =\frac{\mathrm{1,67}\cdot {10}^{-27}\text{kg}\cdot A}{\frac{3}{4}\pi {\left(\mathrm{1,3}\cdot {10}^{-15}\text{m}\right)}^{3}A}\\ \underset{¯}{\rho =\mathrm{1,8}\cdot {10}^{17}\frac{\text{kg}}{{\text{m}}^{\text{3}}}=\mathrm{1,8}\cdot {10}^{14}\frac{\text{g}}{{\text{cm}}^{\text{3}}}}\end{array}$

Aus der Gleichung kann man auch ableiten, dass die Dichte der Kernmaterie für alle Elemente den gleichen Wert hat. Diese Dichte liegt um viele Größenordnungen über der Dichte von „normalen“ Stoffen.