Boxplots

Unter dem 1. Quartil versteht man einen Wert, vor dem mindestens $25\%$ und nach dem höchstens $75\%$ der Werte der Urliste liegen; als 3. Quartil bezeichnet man einen Wert, vor dem mindestens $75\%$ und nach dem höchstens $25\%$ der Werte der Urliste liegen.

Die Boxplotdarstellung ist ein gutes Hilfsmittel für den Vergleich von Verteilungen, da man zum Beispiel erkennt, welchen Bereich (welche Spannweite) die ermittelten Daten einnehmen, ob die Verteilung bezüglich des Medians symmetrisch, rechts- oder linksschief ist.

Ein Boxplot entsteht wie folgt:
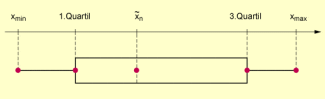
Auf einer Zahlengeraden werden dazu die entsprechenden Werte der zu untersuchenden Zufallsgröße markiert. Über dieser Geraden zeichnet man dann ein vom unteren bis zum oberen Viertelwert reichendes Rechteck (eine Box) und kennzeichnet darin den Zentralwert ${\tilde{x}}_n$ durch einen senkrechten Strich.

Die außerhalb dieses Rechtecks liegenden extremen Beobachtungswerte $x_{\min }$ und $x_{\max }$ werden durch Kreuze markiert. Mitunter werden links und rechts vom Kasten noch Linien gezeichnet, welche die Verteilung außerhalb des Kastens andeuten. Im Allgemeinen werden diese Linien so lang gewählt, dass jeweils nicht mehr als $10\%$ der Daten außerhalb liegen.

Beispiel: Ein Institut beschäftigt 11 Mitarbeiter, deren Gehaltsverteilung aus folgender Tabelle ersichtlich ist:

Um eine Boxplot-Darstellung der Häufigkeitsverteilung zu erhalten, geht man etwa in folgenden Schritten vor:

(1) Ordnen der Werte und Kennzeichnen der fünf Lageparameter

(2) Festlegen eines geeigneten Maßstabs und Darstellen im Boxplot

Der „Kasten“ (die „Box“) wird längs einer Zahlengeraden als ein vom 1. bis zum 3. Quartil reichendes Rechteck gezeichnet, in dem der Median (Zentralwert) durch einen senkrechten Strich gekennzeichnet ist. Den maximalen und den minimalen Wert gibt man durch Punkte oder Kreuze auf der Zahlengeraden an.

Die Darstellung macht deutlich (was im vorliegenden einfachen Fall zwar bereits aus der Tabelle erkennbar, bei einem großen Datenumfang aber wesentlich schwerer zu übersehen ist): Die Gehaltsverteilung ist sehr unausgeglichen – bedingt durch den „Ausreißerwert“ 7500 Euro ist der Abstand von 3. Quartil zum Maximum sehr groß. Die Mehrheit der Gehälter und auch der Median drängen sich auf dem relativ kleinen und sehr niedrigen Intervall von 2000 bis 2500 Euro zusammen.