Grafische Darstellungen mit einem Tabellenkalkulationsprogramm

Die Anleitungen beschränken sich in der Regel auf eine mögliche Variante zur Lösung des jeweiligen mathematischen Problems.

Zur grafischen Darstellung einer Funktion f mit f(x) muss zuerst eine Wertetabelle aufgestellt werden. Mit den Zahlenpaaren der Tabelle wird dann ein Diagramm erstellt. Dabei ist zu beachten, dass

1. das Darstellungsintervall durch die Tabelle vorgegeben wird,
2. die grafische Darstellung der Funktion punktweise erfolgt und deshalb bereits in der Tabelle eine hinreichend kleine Schrittweite vorzugeben ist.

Beispiel: Die Funktion f mit $f\left(x\right)=\frac{2x+1}{x^2+3}$ soll grafisch dargestellt werden.

Schrittfolge zum Erstellen der Wertetabelle:
1. Tabellenkopf vorgeben, z.B. Zelle A1: x; Zelle B1: y

2. Darstellungsintervall festlegen, z.B. $-3\le x\le 3$ mit der Schrittweite 0,5
In Zelle A2 wird der Wert -3 und in Zelle A3 der Wert -2,5 eingetragen. Durch A2 und A3 ist die Schrittweite 0,5 festgelegt. Die Schrittweite ist nun auf die gesamte Tabelle zu übertragen. Dazu werden die Zellen A2 und A3 gemeinsam markiert und an der rechten unteren Ecke nach unten gezogen bis die „3“ erscheint.

3. Funktionswerte ermitteln
In Zelle B2 (der Zelle für den ersten Funktionswert) wird der Funktionsterm durch Zellenbezug definiert. Dabei ist immer mit einem Gleichheitszeichen zu beginnen.

Der Funktionsterm ist nun auf die gesamte Tabelle zu übertragen. Dazu wird Zelle B2 bis zum Ende der Tabelle (B14) aufgezogen.
Es entstehen die Funktionswerte für das vorgegebene Intervall.

Schrittfolge zum Erstellen der grafischen Darstellung der Wertetabelle:
Die grafische Darstellung der Wertepaare kann mithilfe eines zum Kalkulationsprogramm gehörenden „Diagrammassistenten“ erzeugt werden:

1. Der Diagrammassistent wird über die Standard-Symbolleiste oder über Einfügen/Diagramm aufgerufen.

2. Diagrammtyp und Untertyp auswählen
Da es sich bei diesem Beispiel um eine stetige Funktion handelt, ist hier der Diagrammtyp Linien auszuwählen.

3. Darzustellende Daten eingeben
Dazu sind die Karteikarte Datenbereich auszuwählen, das Datenbereich-Feld anzuklicken und die Daten der Spalte B (Funktionswerte) zu markieren. (Die entsprechende Zellenbezeichnung erscheint im Datenbereich-Feld.)
Dann wird die Karteikarte Reihe ausgewählt und das Feld Beschriftung der Rubrikenachse (X) angeklickt. Danach ist die Spalte A (x-Werte) zu markieren.

Wenn nicht bereits erfolgt, kann die Bezeichnung der Kurve ergänzt werden (besonders wichtig, wenn mehrere Kurven in einem Koordinatensystem dargestellt werden sollen). Dazu wird nach Anklicken des Namen-Feldes die Zelle B2 markiert. Der Zelleninhalt erscheint nun als Name.

4. Mit den Diagrammoptionen können vor allem verschiedene Beschriftungen und Gitternetzlinien realisiert werden.

5. Das Diagramm wird nun mit weiter und Ende fertiggestellt.

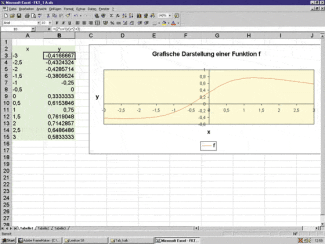
Erscheint der Graph eckig, sind in der Regel zu wenig Wertepaare vorgegeben. Abhilfe kann auch die Formatierung Linie glätten schaffen.

Von den zusätzlich möglichen Formatierungen sei vor allem auf die Stellung der y-Achse verwiesen. Standardmäßig befindet sich die y-Achse immer am linken Diagrammrand. Um das zu ändern, muss die x-Achse (!) formatiert werden:
x-Achse mit der rechten Maustaste anklicken und Achse formatieren/Skalierung auswählen.

Da die y-Achse die x-Achse bei $x=0$ schneiden soll, ist in der Wertetabelle abzuzählen, das wievielte Element $x=0$ ist (im Beispiel das siebente). Diese Zahl ist in das oberste Feld (Größenachse schneidet bei Rubrik-Nr.) einzutragen.

Soll das so angelegte Rechenblatt später zur grafischen Darstellung einer anderen Funktion genutzt werden, ist in Zelle B2 der neue Funktionsterm zu definieren und auf die restlichen Felder der Wertetabelle zu übertragen (siehe oben). Daraufhin wird sofort die dazugehörige grafische Darstellung erzeugt.