Oberflächen von Tabellenkalkulationsprogrammen
Die Oberfläche eines Tabellenkalkulationsprogramms enthält als zentrales Element die Kalkulationstabelle. Um sie herum sind Bedienelemente, wie Menü- und Symbolleisten, Statuszeile und Rollbalken, angeordnet.
In die Zellen der Tabelle werden Zahlen, Daten, Texte, Formeln usw. eingegeben, und mit den Bedienelementen werden diese bearbeitet bzw. formatiert. Weitere Bedienelemente ermöglichen das Navigieren in umfangreichen Kalkulationstabellen, das Markieren und Formatieren von Tabellenteilen.
Oberfläche von Excel
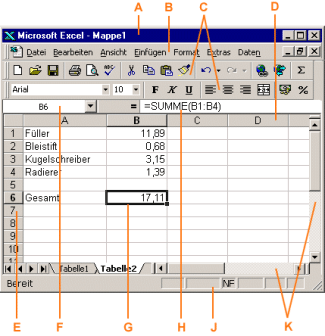
In der folgenden Abbildung ist die Oberfläche von Excel dargestellt, wobei in einige Zellen schon Texte oder Zahlen eingegeben wurden.
Im Einzelnen bedeuten:
- Titelleiste (A)
mit dem Namen des aktuellen Dokuments (hier: „Mappe1“) sowie den Schaltern zum Minimieren, Maximieren und Schließen des Fensters - Menüleiste (B)
mit Pull-Down-Menüs
(enthält Befehle zum Speichern, Drucken, Formatieren, Erstellen von Formeln usw.; durch Anklicken der Menü-Worte werden Menüs geöffnet, die weitere Befehle enthalten) - Symbolleisten (C)
mit Schaltern für häufig verwendete Befehle - Spaltenkopf (D)
zur Bezeichnung der einzelnen Spalten - Zeilenkopf (E)
zur Bezeichnung der einzelnen Zeilen - Namenfeld (F)
(enthält die Bezeichnung der aktuellen Zelle; im Bild ist es die Zelle „B6“, da diese Zelle markiert ist) - Markierungsumrandung (G)
zur Markierung von Zellen oder Bereichen - Bearbeitungsleiste (H)
zum Eingeben bzw. Bearbeiten von Formeln oder anderen Zelleninhalten
(im Bild wird die Formel angezeigt, die sich in der Zelle B6 befindet und das in der Zelle B6 angezeigte Ergebnis erzeugt) - Statuszeile (J)
mit Informationen zu einem gewählten Befehl oder zum „Arbeitszustand“ des Programms - (horizontale und vertikale) Bildlaufleisten (K)
zum Verschieben des sichtbaren Bildausschnitts
-
Benutzeroberfläche des Tabellenkalkulationsprogramms Excel
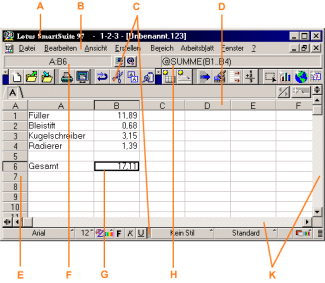
Lotus 1-2-3
Die Oberfläche von Lotus 1-2-3 unterscheidet sich zwar im ersten Eindruck von der Excel-Oberfläche, jedoch sind bei näherem Hinsehen die wichtigsten Funktionselemente genau wie bei Excel (siehe obige Erläuterung der Bedienelemente) vorhanden.
-
Benutzeroberfläche des Tabellenkalkulationsprogramms Lotus 1-2-3
keine Angabe
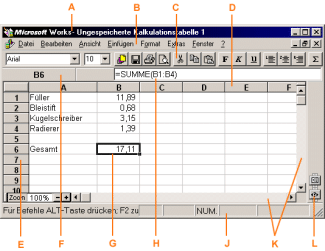
Works
Auch die Oberfläche von Works bietet die gleichen Grundfunktionen wie Excel oder Lotus. Dementsprechend ist auch hier die Oberfläche ähnlich wie bei Excel (siehe obige Erläuterung der Bedienelemente) gestaltet; zusätzlich gibt es ein Symbol zum Öffnen der Hilfeleiste (L).
-
Benutzeroberfläche des Tabellenkalkulationsprogramms Works
keine Angabe

