Proportionalzirkel

Der Proportionalwinkel besteht aus zwei flachen Schenkeln, die sich um einen festen Drehpunkt an einem Ende der Schenkel öffnen oder schließen lassen. Diese Form geht auf GALILEO GALLILEI (1564 bis 1642) zurück und wird deshalb auch als galileischer Typ des Proportionalzirkels bezeichnet.

Eine zweite Form soll auf den Schweizer JOBST BÜRGI (1552 bis 1632) zurückgehen. Bei diesem sogenannten bürgischen Typ befindet sich der Drehpunkt zwischen den Schenkelenden; bei fortgeschrittenen Ausführungen sind zudem Drehpunkt und Schenkellänge verstellbar.

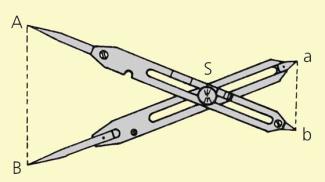
Da diese Proportionalzirkel oftmals für maßstabsgerechte Verkleinerungen verwendet wurden, nannte man sie auch Reduktionszirkel (compasso di reduzione). Einfache Reduktionszirkel mit festen Schenkellängen und ohne Rechenskalen gab es schon vor dem Proportionalzirkel. Sie gestatteten lediglich, Strecken in einem durch ihre Schenkellängen vorherbestimmten Verhältnis ineinander umzuwandeln.

Je nach Verwendungszweck waren auf den Schenkeln der meisten Proportionalzirkel verschiedene Funktionsskalen (z.B. lineare oder logarithmische Skalen, Skalen für Quadratzahlen oder Quadratwurzeln, aber auch Skalen für Kreis-, Flächen- oder Volumenberechnungen) aufgetragen.

Mathematische Grundlagen

Durch Kenntnis der Strahlensätze war man frühzeitig in der Lage, Verhältnisgleichungen zu lösen. Im Normalfall muss dazu die Gleichung nach einem Strahlenabschnitt oder Parallelenabschnitt umgeformt werden, z.B.:
$\frac{\left|\overline{AB}\right|}{\left|\overline{CD}\right|}=\frac{\left|\overline{SB}\right|}{\left|\overline{SD}\right|}\Rightarrow \left|\overline{CD}\right|=\frac{\left|\overline{AB}\right|\cdot \left|\overline{SD}\right|}{\left|\overline{SB}\right|}$

Betrachtet man die Skalen auf den Schenkeln eines geöffneten Proportionalzirkels als Strahlen mit einem gemeinsamen Anfangspunkt, so kann man mithilfe eines Stechzirkels Strahlen- und Parallelenabschnitte als Streckenlängen abgreifen.

Da sich auf beiden Schenkeln Skalen gleicher Einteilung befinden, gilt:
$\frac{\left|\overline{SA}\right|}{\left|\overline{SB}\right|}=\frac{\left|\overline{SC}\right|}{\left|\overline{SD}\right|}=1$

Nach dem Strahlensatz kann nun aus drei bekannten Strecken mithilfe des Stechzirkels am Proportionalzirkel die vierte Strecke und somit die gesuchte Zahl oder Größe wie folgt bestimmt werden:

1. Die Strecke $\overline{SB}$ wird mit dem Stechzirkel abgegriffen und von S aus auf den anderen Schenkel abgetragen, es entsteht der Punkt A.
2. Die Strecke $\overline{SD}$ wird mit dem Stechzirkel abgegriffen und ebenfalls auf den anderen Schenkel von S aus abgetragen, es entsteht der Punkt C.
3. Die Strecke $\overline{AB}$ wird in den Stechzirkel genommen und der Proportionalzirkel so weit geöffnet, dass die Zirkelspanne mit dem Abstand der Punkte A und B übereinstimmt.
4. Die gesuchte Strecke $\overline{CD}$ kann nun mit dem Stechzirkel am geöffneten Proportionalzirkel abgegriffen werden.

Mithilfe des Proportionalzirkels war es auch möglich zu multiplizieren und zu dividieren, wenn anstelle linearer Skalen logarithmische Skalen verwendet wurden.

Durch Anwenden der Logarithmengesetze wird die Multiplikation auf die Addition von Strecken und die Division auf die Subtraktion von Strecken zurückgeführt. Die Strecken werden dazu mit einem Stechzirkel abgegriffen und addiert bzw. subtrahiert.

Proportionalzirkel mit logarithmischen Skalen entsprachen somit den ersten Rechenstäben.