Lineare Gleichungssysteme

Gegeben sei folgendes Gleichungssystem aus drei Gleichungen mit den drei Unbekannten x, y und z:
$\begin{array}{l}{\text{a}}_{\text{1}}\text{x}+{\text{b}}_{\text{1}}\text{y}+{\text{c}}_{\text{1}}\text{z}={\text{d}}_{\text{1}}\\ {\text{a}}_{\text{2}}\text{x}+{\text{b}}_{\text{2}}\text{y}+{\text{c}}_{\text{2}}\text{z}={\text{d}}_{\text{2}}\\ {\text{a}}_{\text{3}}\text{x}+{\text{b}}_{\text{3}}\text{y}+{\text{c}}_{\text{3}}\text{z}={\text{d}}_{\text{3}}\end{array}$
Die Lösung eines solchen Gleichungssystems ist abhängig von den Werten für die Koeffizienten der Unbekannten sowie der Konstanten ${\text{d}}_{\text{i}}$.

Zum Lösen des Gleichungssystems betrachtet man zunächst die Koeffizienten der Unbekannten und schreibt sie als sogenannten Determinante D auf.
Es ist dann:
D = $\left|\begin{array}{l}{\text{a}}_{\text{1}}{\text{b}}_{\text{1}}{\text{c}}_{\text{1}}\\ {\text{a}}_{\text{2}}{\text{b}}_{\text{2}}{\text{c}}_{\text{2}}\\ {\text{a}}_{\text{3}}{\text{b}}_{\text{3}}{\text{c}}_{\text{3}}\end{array}\right|$

Den Wert für D erhält man nach folgender Gleichung:
$\text{D}=\left({\text{a}}_{\text{1}}{\text{b}}_{\text{2}}{\text{c}}_{\text{3}}\right)+\left({\text{b}}_{\text{1}}\text{c}{}_{\text{2}}{\text{a}}_{\text{3}}\right)+\left({\text{c}}_{\text{1}}\text{a}{}_{\text{2}}{\text{b}}_{\text{3}}\right)-\left({\text{a}}_{\text{3}}{\text{b}}_{\text{2}}{\text{c}}_{\text{1}}\right)-\left({\text{b}}_{\text{3}}{\text{c}}_{\text{2}}{\text{a}}_{\text{1}}\right)-\left({\text{c}}_{\text{3}}{\text{a}}_{\text{2}}{\text{b}}_{\text{1}}\right)$
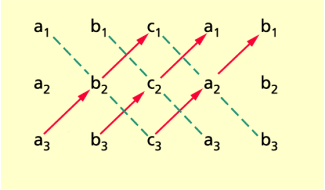
Man erhält diese Gleichung, wenn man hinter die Determinante D die ersten beiden Spalten nochmals schreibt und dann die Produkte der Glieder der drei nach rechts fallenden Diagonalen addiert und davon die Produkte der nach rechts steigenden Diagonalen subtrahiert (Bild 1).
Dieses Vorgehen nennt man nach dem französischen Mathematiker PIERRE-FREDERIC SARRUS (1796 bis 1861) sarrussche Regel.

Die zur Unbekannten x gehörende Determinante $D_x$ erhält man, wenn man in D die Werte für $a_i$ durch die entsprechenden ${\text{d}}_{\text{i}}$ ersetzt, also
${\text{D}}_{\text{x}}=\left({\text{d}}_{\text{1}}{\text{b}}_{\text{2}}{\text{c}}_{\text{3}}\right)+\left({\text{b}}_{\text{1}}{\text{c}}_{\text{2}}{\text{d}}_{\text{3}}\right)+\left({\text{c}}_{\text{1}}{\text{d}}_{\text{2}}{\text{b}}_{\text{3}}\right)-\left({\text{d}}_{\text{3}}{\text{b}}_{\text{2}}{\text{c}}_{\text{1}}\right)-\left({\text{b}}_{\text{3}}{\text{c}}_{\text{2}}{\text{d}}_{\text{1}}\right)-\left({\text{c}}_{\text{3}}{\text{d}}_{\text{2}}{\text{b}}_{\text{1}}\right)$
Analog erhält man:
$\begin{array}{l}{\text{D}}_{\text{y}}=\left({\text{a}}_{\text{1}}{\text{d}}_{\text{2}}{\text{c}}_{\text{3}}\right)+\left({\text{d}}_{\text{1}}{\text{c}}_{\text{2}}{\text{a}}_{\text{3}}\right)+\left({\text{c}}_{\text{1}}{\text{a}}_{\text{2}}{\text{d}}_{\text{3}}\right)-\left({\text{a}}_{\text{3}}{\text{d}}_{\text{2}}{\text{c}}_{\text{1}}\right)-\left({\text{d}}_{\text{3}}{\text{c}}_{\text{2}}{\text{a}}_{\text{1}}\right)-\left({\text{c}}_{\text{3}}{\text{a}}_{\text{2}}{\text{d}}_{\text{1}}\right)\\ {\text{D}}_{\text{z}}=\left({\text{a}}_{\text{1}}{\text{b}}_{\text{2}}{\text{d}}_{\text{3}}\right)+\left({\text{b}}_{\text{1}}{\text{d}}_{\text{2}}{\text{a}}_{\text{3}}\right)+\left({\text{d}}_{\text{1}}{\text{a}}_{\text{2}}{\text{b}}_{\text{3}}\right)-\left({\text{a}}_{\text{3}}{\text{b}}_{\text{2}}{\text{d}}_{\text{1}}\right)-\left({\text{b}}_{\text{3}}{\text{d}}_{\text{2}}{\text{a}}_{\text{1}}\right)-\left({\text{d}}_{\text{3}}{\text{a}}_{\text{2}}{\text{b}}_{\text{1}}\right)\end{array}$

Als Lösungen des Gleichungssystems erhält man nun
$\text{x}=\frac{{\text{D}}_{\text{x}}}{\text{D}}\text{y}=\frac{{\text{D}}_{\text{y}}}{\text{D}}\text{z}=\frac{{\text{D}}_{\text{z}}}{\text{D}}$
Dieses Vorgehen heißt auch cramersche Regel, nach GABRIEL CRAMER, der dieses Verfahren 1750 begründete.
Voraussetzung für die Existenz von Lösungen ist $\text{D}\ne \text{0}$.
Ist D = 0 und mindestens eine Zählerdeterminante $D_x,D_{y}oder{D}_z$ von Null verschieden, so widersprechen sich die Gleichungen.
Gilt hingegen $D=D_x=D_y=D_z=0$, so sind die Gleichungen linear abhängig.

Die cramersche Regel gilt auch für Gleichungssysteme mit mehr als drei Unbekannten. Allerdings kann man dann die Determinanten nicht mehr so einfach berechnen, weil die Regel von SARRUS nur für 3-reihige Determinanten gilt.
Durch Entwicklung in Unterdeterminanten kann man aber eine n-reihige Determinante auf (n – 1)-reihige Determinanten zurückführen und so schließlich zu 3-reihigen Determinanten gelangen.
Die Entwicklung in Unterdeterminanten wird am Beispiel einer 4-reihigen Determinante gezeigt: Die Determinante
$D=\left|\begin{array}{l}{a}_1{b}_1{c}_1{d}_1\\ a_2{b}_2{c}_2{d}_2\\ a_3{b}_3{c}_3{d}_3\\ a_4{b}_4{c}_4{d}_4\end{array}\right|$

wird nach der ersten Spalte in Unterdeterminanten entwickelt.
Dann gilt:
$D=a_1\cdot \left|\begin{array}{l}{b}_2{c}_2{d}_2\\ b_3{c}_3{d}_3\\ b_4{c}_4{d}_4\end{array}\right|-a_2\cdot \left|\begin{array}{l}{b}_1{c}_1{d}_1\\ b_3{c}_3{d}_3\\ b_4{c}_4{d}_4\end{array}\right|+a_3\cdot \left|\begin{array}{l}{b}_1{c}_1{d}_1\\ b_2{c}_2{d}_2\\ b_4{c}_4{d}_4\end{array}\right|-a_4\cdot \left|\begin{array}{l}{b}_1{c}_1{d}_1\\ b_2{c}_2{d}_2\\ b_3{c}_3{d}_3\end{array}\right|$