Ballistisches Pendel

Was ist ein ballistisches Pendel?
Unter einem ballistischen Pendel (Ballistik ist die Lehre von den Geschossbahnen) versteht man eine Anordnung, mit der man z.B. die Geschwindigkeit eines Geschosses bestimmen kann. Sie besteht aus einem Pendelkörper, in dem das Geschoss stecken bleibt und der durch das Geschoss bewegt wird. Unter Nutzung des Impulserhaltungssatzes und weiterer Gesetze der Mechanik lässt sich die Geschossgeschwindigkeit ermitteln.

Ermittlung der Geschossgeschwindigkeit

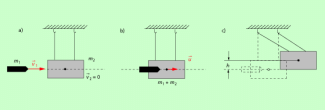
Bild 2 zeigt die Experimentieranordnung und die Bewegung des Pendels in verschiedenen Phasen. Das Geschoss bleibt in dem Holzklotz stecken. Beide Körper bewegen sich mit einer gemeinsamen Geschwindigkeit weiter. Es liegt somit ein unelastischer Stoß vor.
Für das System Pendelkörper - Geschoss gilt der Impulserhaltungssatz in folgender Form:

$\begin{array}{l}{m}_{\text{G}}\cdot v_{\text{G}}=(m_{\text{G}}+m_{\text{P}})u\\ \text{Dabei ist }{m}_{\text{G}}\text{ die Masse des Geschosses}\text{,}\\ v_{\text{G}}\text{ die Geschwindigkeit des Geschosses}\text{,}\\ m_{\text{P}}\text{ die Masse des Pendelkörpers und }\\ u\text{ die gemeinsame Geschwindigkeit}\text{.}\\ \text{Die Umstellung nach }{v}_{\text{G}}\text{ ergibt:}\\ v_{\text{G}}=\frac{m_{\text{G}}+m_{\text{P}}}{m_{\text{G}}}\cdot u\end{array}$

Die gemeinsame Geschwindigkeit u lässt sich in folgender Weise bestimmen: Durch das Eindringen des Geschosses gerät das ballistische Pendel in Schwingungen. Seine kinetische Energie wird in potenzielle Energie umgewandelt und umgekehrt. Der Schwerpunkt des Pendels erreicht eine maximale Höhe h. Wird die Reibung vernachlässigt, dann gilt für die Pendelschwingungen der Energieerhaltungssatz der Mechanik:

$\begin{array}{l}\frac{1}{2}(m_{\text{G}}+m_{\text{P}})\cdot u^2=(m_{\text{G}}+m_{\text{P}})\cdot g\cdot h\\ \text{Die Umstellung der Gleichung nach }u\text{ ergibt:}\\ u=$ \sqrt{2\cdot g\cdot h}$\end{array}$

Setzt man die Gleichung für u in die obige Gleichung für die Geschossgeschwindigkeit ein, so erhält man:

$v_{\text{G}}=\frac{m_{\text{G}}+m_{\text{P}}}{m_{\text{G}}}\cdot \sqrt{2g\cdot h}$

Eine andere Möglichkeit besteht darin, den Holzkörper auf eine ebene Fläche zu legen. Dringt das Geschoss ein, so bewegt sich der Körper auf der ebenen Fläche und kommt durch die Reibungskraft zum Stillstand. Es wird also die ursprünglich vorhandene kinetische Energie in Reibungsarbeit umgewandelt. Damit gilt:

$\begin{array}{l}\frac{1}{2}(m_G+m_P)u^2=\mu \cdot (m_G+m_P)\cdot g\cdot s\\ \text{Die Umstellung der Gleichung nach}u\text{ergibt:}\\ u=\sqrt{2\mu \cdot g\cdot s}\\ \mu \text{Reibungszahl}\\ g\text{Ortsfaktor (Fallbeschleunigung)}\\ s\text{Weg des Holzklotzes bis zum Stillstand}\end{array}$

Auch auf diese Weise kann man die Geschwindigkeit u ermitteln und damit die Geschossgeschwindigkeit berechnen.

Eine dritte Möglichkeit ist die Bestimmung der Schwingungsweite des Pendels. Daraus lässt sich die Geschwindigkeit des Pendels ermitteln und damit die Geschoßgeschwindigkeit berechnen.