Genauer gekennzeichnet sind mechanische Wellen in dem Artikel “Mechanische Wellen“.

Wir beschränken uns nachfolgend auf die Charakterisierung von sinusförmigen Wellen.

Beschreibung mechanischer Wellen mit Diagrammen

Ähnlich wie mechanische Schwingungen lassen sich mechanische Wellen durch Diagramme beschreiben.

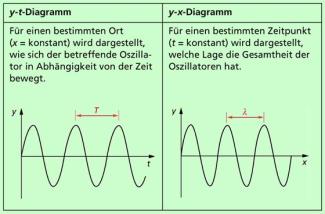
Wird für einen bestimmten Ort x (x = konstant) dargestellt, wie sich ein Schwinger oder Oszillator an diesem Ort in Abhängigkeit von der Zeit bewegt, so erhält man wie bei einer Schwingung ein y-t-Diagramm. y ist dabei die Auslenkung (Elongation), t die Zeit (Bild 2 links). Beschrieben wird mit diesem Diagramm die Bewegung eines Schwingers. Abgelesen werden kann aus dem y-t-Diagramm die Auslenkung (Elongation) y zu verschiedenen Zeiten t. Der Abstand zweier benachbarter Wellenberge ist gleich der Schwingungsdauer (Periodendauer) T des Schwingers.

Wird für einen bestimmten Zeitpunkt t (t = konstant) dargestellt, welche Lage die einzelnen Schwinger zu diesem Zeitpunkt haben, so erhält man ein y-x-Diagramm. y ist dabei wieder die Auslenkung (Elongation), x der Ort des jeweiligen Schwingers (Bild 2 rechts). Statt des Ortes x verwendet man zur Beschreibung manchmal auch den Weg s. Beschrieben wird mit diesem Diagramm der jeweilige Schwingungszustand vieler Schwinger zu einem bestimmten Zeitpunkt. Man hat also eine „Momentaufnahme“ einer Welle vor sich. Abgelesen werden kann aus dem y-x-Diagramm die momentane Auslenkung y eines Schwingers an einem bestimmten Ort x, wobei man x (oder s) von einem (willkürlich) gewählten Nullpunkt aus misst. Der Abstand zweier benachbarter Wellenberge ist gleich der Wellenlänge.

Zur vollständigen Beschreibung einer Welle sind immer beide Diagramme erforderlich.

Beschreibung mechanischer Wellen mit physikalischen Größen

Da bei einer Welle jeder einzelne Oszillator mechanische Schwingungen ausführt, können zur Beschreibung von Wellen zunächst solche physikalischen Größen genutzt werden, die man auch zur Beschreibung von Schwingungen verwendet. Es handelt sich dabei um die Auslenkung (Elongation), die Amplitude, die Schwingungsdauer (Periodendauer) und die Frequenz. Diese Größen sind in der nachfolgenden Übersicht näher charakterisiert.

Darüber hinaus wird eine mechanische Welle mit den physikalischen Größen Wellenlänge und Ausbreitungsgeschwindigkeit beschrieben.
Die Wellenlänge einer Welle gibt den Abstand zweier benachbarter Schwinger an, die sich im gleichen Schwingungszustand befinden.

Gleiche Schwingungszustände sind z. B. zwei benachbarte Wellenberge oder zwei benachbarte Wellentäler. Ihr Abstand voneinander ist gleich der Wellenlänge (Bild 2).
Die Ausbreitungsgeschwindigkeit einer Welle ist die Geschwindigkeit, mit der sich ein Schwingungszustand, z. B. ein Wellenberg, im Raum ausbreitet. Da ein bestimmter Schwingungszustand identisch ist mit einer bestimmten Phase einer Welle, spricht man auch von Phasengeschwindigkeit .

Messen kann man die Ausbreitungsgeschwindigkeit oder Phasengeschwindigkeit z. B. so, dass man bestimmt, wie schnell sich ein Wellenberg oder ein Wellental ausbreitet. Davon zu unterscheiden ist die Gruppengeschwindigkeit, mit der sich z.B. eine ganze Wellengruppe ausbreitet. Beide Geschwindigkeit können, müssen aber nicht gleich groß sein.

In der nachfolgenden Übersicht werden Wellenlängen und Ausbreitungsgeschwindigkeiten für einige mechanische Wellen angegeben. Man beachte, dass es sich dabei teilweise um die Angabe von Größenordnungen handelt.

Zwischen der Ausbreitungsgeschwindigkeit einer Welle, ihrer Wellenlänge und der Frequenz besteht ein enger Zusammenhang. Für alle mechanischen Wellen gilt:

$\begin{array}{l}v=\lambda \cdot f\\ v\text{Ausbreitungsgeschwindigkeit der Welle}\\ \lambda \text{Wellenlänge}\\ f\text{Frequenz}\text{, mit der Oszillatoren schwingen}\end{array}$

Dabei ist zu beachten, dass bei der Ausbreitung von Wellen die Frequenz immer gleich bleibt, sich aber beim Übergang von einem Stoff in einen anderen oder auch bei der Ausbreitung in einem Stoff unterschiedlicher Temperatur oder verschiedener Dichte die Ausbreitungsgeschwindigkeit ändern kann. Das ist verbunden mit einer Änderung der Wellenlänge. Mit Vergrößerung der Ausbreitungsgeschwindigkeit vergrößert sich die Wellenlänge, mit Verkleinerung der Ausbreitungsgeschwindigkeit verkleinert sie sich.

Beschreibung mechanischer Wellen mit der Wellengleichung

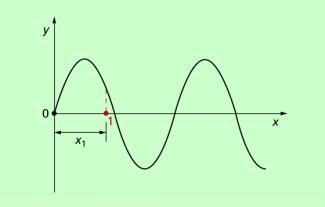
Ähnlich wie mechanische Schwingungen kann man auch mechanische Wellen mathematisch beschreiben. Wir gehen dabei wieder davon aus, dass jeder einzelne Schwinger eine harmonische (sinusförmige) Schwingung ausführt. Die Gesamtheit der Schwinger zu einem bestimmten Zeitpunkt ist im y-x-Diagramm dargestellt (Bild 3). Für jeden Oszillator der sinusförmigen Welle gilt dann die Schwingungsgleichung :

$\begin{array}{l}y=y_{\max }\cdot \sin (\omega \cdot t+\varphi )\\ \text{Für den Punkt 0 (Bild 3) setzen wir}\varphi =0.\\ \text{Punkt 1 (Bild 3) hat von 0 den Abstand}{x}_1.\text{Die Zeit}\text{,}\\ \text{in der die Welle von 0 bis}{x}_1\text{gelangt}\text{, sei}{t}_1.\\ \text{Dann ist wegen}\varphi =\omega \cdot t\text{der Phasenunterschied}\\ \text{zwischen den Punkten 0 und 1}\\ {\varphi }_1=-\omega \cdot t_1\\ \text{Die Schwingung in Punkt 1 fängt um die Zeit}{t}_1\\ \text{später an als im Punkt 0}\text{. Damit erhält man für die}\\ \text{Kennzeichnung des Zustandes im Punkt 1:}\\ y_1=y_{\max }\cdot \sin (\omega \cdot t+{\varphi }_1)\text{und mit}{\varphi }_1=-\omega \cdot t_1:\\ y_1=y_{\max }\cdot \sin \omega (t-t_1)\text{(1)}\\ \text{Die Zeit}{t}_1\text{kann man mithilfe der Ausbreitungsgeschwindigkeit}\\ \text{ausdrücken:}{t}_1=\frac{x_1}{v}\\ \text{Eingesetzt in (1) ergibt:}\\ y_1=y_{\max }\cdot \sin \omega \left(t-\frac{x_1}{v}\right)\end{array}$

Diese Gleichung gilt nicht nur für den beliebig herausgegriffenen Punkt 1, sondern auch für beliebige andere Punkt 2, 3, ...

$\begin{array}{l}\text{Setzt man also}{x}_1=x,\text{so erhält man als Wellengleichung:}\\ y=y_{\max }\cdot \sin \omega \left(t-\frac{x}{v}\right)\end{array}$

Diese Wellengleichung wird meist in etwas anderer Form angegeben, die man aus der oben genannten Gleichung herleiten kann.

$\begin{array}{l}\text{Mit}\omega =\frac{2\pi }{T}\text{erhält man die Gleichung:}\\ y=y_{\max }\cdot \sin 2\pi \left(\frac{t}{T}-\frac{x}{v\cdot T}\right)\\ \text{Mit}T=\frac{1}{f}\text{und}\frac{v}{f}=\lambda \text{folgt:}\\ y=y_{\max }\cdot \sin 2\pi \left(\frac{t}{T}-\frac{x}{\lambda }\right)\\ y\text{Elongation (Auslenkung)}t\text{Zeit}\\ y_{\max }\text{Amplitude}x\text{Ort}\\ T\text{Schwingungsdauer}\lambda \text{Wellenlänge}\end{array}$

Die Auslenkung ist also eine Funktion der Zeit t und des Ortes x. Damit wird mit dieser Gleichung das erfasst, was in einem y-t- und einem y-x-Diagramm dargestellt ist: