Das Bändermodell

Das Bändermodell für Festkörper

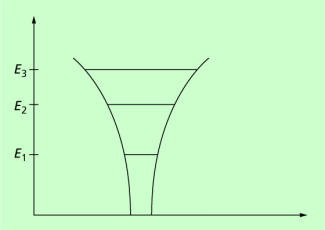
Vom bohrschen Atommodell her ist bekannt, dass in freien Atomen die Elektronen diskrete Bahnen besitzen. Zu einer Bahn gehört eine vom speziellen Atom abhängende charakteristische Energie. In verschiedene Bahnen besitzen die Elektronen verschiedene Energien. Andere Energiewerte als die auf den erlaubten Bahnen kann das an ein Atom gebundene Elektron nicht haben. Folglich sind die möglichen Energien eine diskrete Folge, deren größter Wert die Ionisierungsenergie ist. Bild 1 zeigt ein sogenanntes Trichtermodell mit den zugelassenen Energieniveaus und den dazwischen liegenden verbotenen Bereichen. Man spricht auch von einem Energieniveauschema.

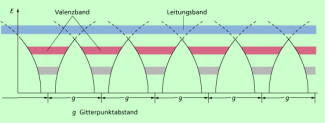
In einem Festkörper mit einer großen Anzahl von Atomen treten durch die Wechselwirkungen nicht mehr diskrete Energieniveaus, sondern relativ breite Energiebereiche auf, die man als Energiebänder bezeichnet.
Innerhalb eines Bandes können die zugehörigen Elektronen einen Energiewert zwischen dem tiefsten (Bandunterkante) und dem höchsten (Bandoberkante) annehmen. Elektronen eines Bandniveaus haben in der Regel auch in benachbarten Atomen verschieden hohe Energie.
Wie man aus dem Bild 2 anschaulich entnehmen kann, ist es möglich, dass sich von einer bestimmten Höhe der Energie an die Potenzialtrichter überschneiden und die Energiebänder durchgehend werden.
Ladungen, die sich in derartigen Bändern befinden, sind also keinem Gitterpunkt mehr fest zugeordnet, sie bewegen sich durch das gesamte Gitter.
Das erste Band mit einer derartigen Eigenschaft nennt man das Leitungsband (Bild 2). Nach oben wird die Energie der Elektronen durch die so genannte Ablösearbeit begrenzt. Das ist der Energiewert, bei dem die Elektronen durch die Außenfläche des Kristalls treten und die Gitterbindung verlieren (Elektronenemission).

Das letzte Energieband, dessen untere Kante unterhalb der Überschneidung der einzelnen Potenzialtrichter liegt, heißt Valenzband V. In ihm befinden sich die Elektronen, die einzelnen Atomen noch zugeordnet sind, aber gleichzeitig den größten Kernabstand besitzen. Sie sind für die möglichen chemischen Bindungen verantwortlich, woraus sich die Bandbezeichnung ableitet.

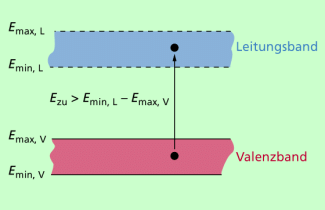
Für die Beschreibung elektrischer Vorgänge reicht es völlig aus, Valenzband und Leitungsband zu betrachten. Wie man vom bohrschen Atommodell weiß, ist zum Anheben eines Elektrons auf ein höheres Energieniveau eine Energiezufuhr erforderlich. Analog liegen die Verhältnisse auch im Kristallgitter. Um ein Elektron aus dem Valenzband in das Leitungsband zu heben, ist ihm ebenfalls Energie zuzuführen. Das kann z.B. durch Erwärmen, Zufuhr von Lichtenergie oder elektrischer Energie erfolgen.
Anders jedoch als im freien Einzelatom, in dem die erforderliche Energie stets den gleichen Wert für den gleichen Bahnübergang hat, ist die erforderliche minimale Energie durch die Energiedifferenz zwischen der unteren Bandkante des Leitungsbandes und der oberen des Valenzbandes (Bild 3) bestimmt.

Leiter, Halbleiter und Isolatoren im Bändermodell

Die gegenseitige Anordnung von Valenz- und Leitungsband bestimmt das elektrische Verhalten der Festkörper (Bild 4).
In den Metallen liegt die unter Bandkante des Valenzbandes unterhalb der Überschneidung der Potenzialtrichter, die obere darüber. Das Leitungsband hat deshalb eine Überschneidungszone mit dem Valenzband. Damit stehen im Leitungsband der Metalle auch ohne äußere Energiezufuhr ständig Elektronen zur Verfügung. Beim Anlegen einer Spannung fließt ein Strom.
In den Halbleitern hat der Abstand der beiden Bandkanten meist die Größenordnung von 1 eV und bleibt unter 3 eV. Das bedeutet, dass bei tiefen Temperaturen das Leitungsband praktisch leer, das Valenzband voll besetzt ist: Das Material verhält sich wie ein Isolator. Bei Zimmertemperatur kann die erforderliche Mindestenergie aber aufgebracht werden, es gehen Elektronen aus dem Valenzband ins Leitungsband über, das Material wird leitend. Dieser Vorgang ist noch von einem zweiten begleitet, der weiter unten aufgegriffen wird.
Bei Isolatoren ist das Leitungsband weitgehend leer, der Abstand der Bandkanten ist größer als 3 eV und liegt meist in einer Größenordnung von etwa 7 eV.

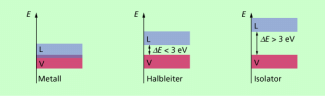
Die Eigenleitung bei Halbleitern

Weiter oben wurde bereits darauf hingewiesen, dass im halbleitenden Material der Elektronenübergang aus dem Valenz- ins Leitungsband nicht allein abläuft. Anders als in den Metallen, in denen sich die beiden Bänder überlappen, also sich im Leitungsband Elektronen aufhalten, die energetisch von solchen des Valenzbandes nicht zu unterscheiden sind, sodass ein solcher Wechsel keine Änderung der Ladungsmengen nach sich zieht, bleibt im Halbleiter im Valenzband zunächst eine unbesetzte Stelle zurück.
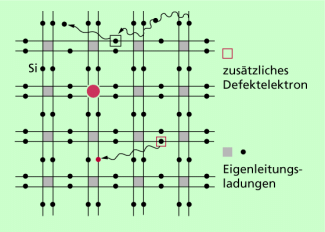
Da bei Energiezufuhr sich der Elektronenaufstieg ins Leitungsband an vielen Stellen vollzieht, entsteht im Valenzband an vielen Gitterplätzen ein positiv zurück bleibender Atomrumpf. Da die in das Leitungsband aufgestiegenen Elektronen infolge von Wechselwirkungen untereinander oder mit dem Kristallgitter dabei einen Teil ihrer ursprünglichen Energie verlieren, müssen sie in das energieärmere Valenzband zurückkehren. Nun wird ein zurückkehrendes Elektron in der Regel nicht wieder genau dorthin kommen, wo es herkam. Die Folge davon ist, dass sich die zu einem gegebenen Zeitpunkt ergebende Verteilung der positiven Rumpfstellen im Gitter fortwährend ändert. Das entspricht formal einer Eigenbeweglichkeit dieser Rümpfe, da zu verschiedenen Zeiten positive Stellen an verschiedenen Gitterorten auftreten. Diese positiven Gitterrümpfe nennt man positive Löcher oder Defektelektronen.
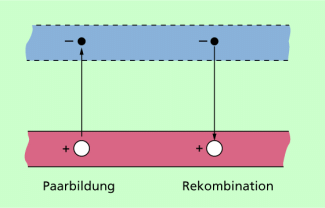
In Bild 5 ist dieser Vorgang veranschaulicht. Man nennt die Entstehung eines Elektrons und eines positiven Lochs infolge des Elektronenübergangs vom Valenz- zum Leitungsband eine Paarbildung. Der entgegengesetzte Vorgang, bei dem ein Elektron des Leitungsbandes nach Energieabgabe ins Valenzband zurückkehrt und dort wieder in das Gitter eingebunden wird, heißt Rekombination. Paarbildung und Rekombination befinden sich in einem dynamischen Gleichgewicht. Das bedeutet, dass je Zeiteinheit die Anzahl beider Vorgänge gleich ist. Die Anzahl beweglicher Ladungsträger in beiden Bändern nimmt mit der Temperatur zu. Der hier geschilderte Vorgang spielt sich in dieser Form allerdings nur in solchen Halbleitern ab, die keine (zumindest praktisch keine) Atome eines anderen Stoffes im Kristallgitter haben.

Den Leitungsmechanismus, der in extrem reinen Halbleitern allein durch die in gleicher Zahl vorhandenen Elektronen und Defektelektronen möglich ist, nennt man Eigenleitung.
Sie ist in den verschiedenen Halbleiterwerkstoffen unter sonst gleichen Bedingungen verschieden intensiv.
Germanium mit einem Bandabstand von 0,72 eV hat bei 300 K (also 27 °C) eine wesentlich stärkere Eigenleitung als Silicium mit einem Bandabstand von 1,1 eV. Denn bei der gleichen Temperatur können im Germanium mehr Elektronen aus dem Valenz- ins Leitungsband gehoben werden, da die erforderliche Energieanhebung kleiner ist, also mit der gleichen zugeführten Energie im Germanium mehr Elektronen als im Silicium in das Leitungsband kommen.

Die Störstellenleitung

Bei der Störstellenleitung kann es sich um eine n-Leitung (Überschussleitung) oder um eine p-Leitung (Mangelleitung) handeln.

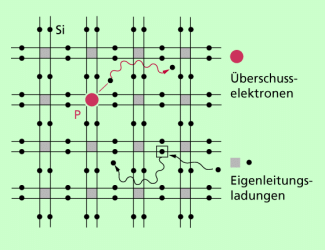
n-Leitung : Baut man in einen zunächst extrem rein hergestellten Halbleitereinkristall mittels spezieller Verfahren (z.B. Diffusion, Ionenimplantation) Atome eines anderen Elements ein, so erzeugen diese Störungen im Kristallgitter. Wählt man für diese Störstellen etwa Atome mit 5 Außenelektronen, so ist an der Einbaustelle mehr vorhanden als für den Gitteraufbau erforderlich, denn im Halbleiter, der 4 Außenelektronen hat, bildet jedes Atom mit 4 weiteren je eine Elektronendoppelbindung, sodass die letzte Schale mit 8 Elektronen besetzt ist und damit ein sehr stabiles Gitter liefert ( Bild 6).
Ist das eingebaute Störstellenatom so ausgewählt, dass sein Valenzband dicht unter dem Leitungsband des Halbleiters liegt, so genügt bereits eine minimale Energie, um das überzählige Elektron in das Valenzband des Halbleiters zu transportieren. Die übrigen 4 Elektronen werden über die Gitterbindung fest am eingebauten Platz gehalten.
Hat man z.B. Phosphor gewählt, so beträgt die Energiedifferenz der beiden Bänder nur 0,044 eV. Die stehen aber bei normaler Umgebungstemperatur zur Verfügung.

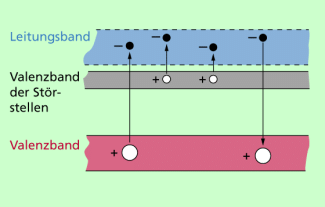
Dieses Störstellenatom liefert nach dem Verlust des 5. Elektrons an das Valenzband natürlich kein positives Loch, denn wegen der Umgebungsbedingungen sind die Elektronenenergien im Leitungsband zu groß für eine Rekombination im Valenzband der Störstelle. Dort bildet sich lediglich ein ortsfestes negatives Ion. Bild 7 versucht diese Verhältnisse zu veranschaulichen.
Neben den Elektronen und Defektelektronen aus dem Mechanismus der Eigenleitung kommt nun je Störstelle ein Elektron hinzu. Das bisher bestehende Gleichgewicht zwischen der Anzahl der Elektronen und der Defektelektronen wird nun zugunsten der Elektronen verschoben.
Damit ergibt sich folgende Ladungsträgerbilanz:

Wegen der größeren Zahl freier negativer Ladungen wird diese durch die Störstellen ausgelöste Situation auch Überschussleitung genannt.
Das Halbleitermaterial verfügt jedoch nur dann über einen dominierend von Elektronen geprägten Leitungsmechanismus, wenn das Verhältnis $\frac{N_{ges}^{-}}{N_{ges}^{+}}>1000$ ist. Eine derartige Forderung lässt sich aber nur innerhalb eines bestimmten Temperaturbereichs realisieren, denn die Anzahl der Ladungen aus der Eigenleitung zeigt eine starke Temperaturabhängigkeit. Oberhalb des zulässigen Temperaturbereichs strebt $\frac{N_{ges}^{-}}{N_{ges}^{+}}\to 1$. Unterhalb des genannten Bereichs passiert das gleiche, denn wegen der sinkenden Energie wird eine Rekombination zum Valenzband der Störstellen möglich, so dass wiederum nur die Eigenleitung verbliebe.
Die eingebauten Störstellen, die ein zusätzliches Leitungselektron liefern, nennt man Donatoren, den Vorgang des Einbaus von Störstellen Dotieren. Weitere Donatoren könnten neben Phosphor auch Arsen und Antimon sein.

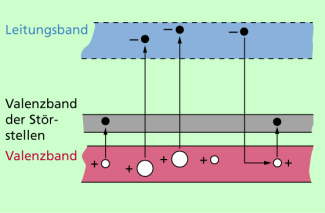
p-Leitung: Es ist auch möglich, in ein extrem reines Halbleitergitter Störstellen mit nur 3 Außenelektronen einzubauen. Wählt man nun solche Atome, deren Valenzband dicht über dem der Halbleiteratome liegen, so wird bereits bei sehr geringen Energien ein Teil der Paarbildungselektronen in das Valenzband der Störstellen eingebaut, sodass dieses voll ist. Die dazu „verbrauchten“ Elektronen fehlen für die Rekombination, sodass sich im Valenzband der Halbleiteratome mehr Löcher befinden als in deren Leitungsband Elektronen. Bild 8 versucht die Situation zu veranschaulichen.
Die Fremdatome oder Störstellen, die jeweils ein Elektron fest binden, verhalten sich im Gitter wie ein negatives ortsfestes Ion. Man bezeichnet sie als Akzeptoren, den entstehenden Leitungsmechanismus als Elektronen-Mangelleitung oder Löcherleitung.
Ihre Ladungsträgerbilanz weist eine Überzahl positiver Löcher entsprechend der Anzahl der eingebauten Störstellen auf.
In einer stark vereinfachten ebenen Darstellung des Kristallgitters kann man mit Bild 13 eine Vorstellung gewinnen.