Der Compton-Effekt

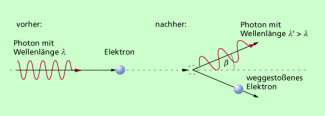
Photonen können mit Elektronen wechselwirken. Besonders deutlich zeigt sich das, wenn man Grafit Röntgenstrahlung aussetzt: Grafit enthält Elektronen mit vernachlässigbar kleiner Austrittsarbeit. Man kann diese Elektronen als frei oder als lose gebunden ansehen. Trifft ein Röntgenphoton auf ein freies Elektron, so kommt zu einer Wechselwirkung, so wie sie in Bild 1 dargestellt ist. Man spricht von einer Streuung des Photons. Nach der Streuung hat das Photon eine kleinere Frequenz und damit eine größere Wellenlänge als zuvor. Es besitzt damit auch eine kleinere Energie. Die Energieverringerung beim Photon ist nach dem Energieerhaltungssatz gleich der Energievergrößerung beim Elektron. Für das System Photon - Elektron gilt auch der Impulserhaltungssatz. Auf das Elektron wird nicht nur Energie, sondern auch Impuls übertragen. Man kann sich folglich die Wechselwirkung zwischen Photon und Elektron energetisch wie einen elastischen Stoß vorstellen.
Entdeckt wurde dieser Effekt im Jahre 1922 von dem US-amerikanischen Physiker ARTHUR HOLLY COMPTON (1892-1962). Er wird nach ihm als COMPTON-Effekt bezeichnet. Für die Entdeckung dieses Effekts wurde COMPTON 1927 mit dem Nobelpreis für Physik geehrt.

Um die Änderung der Wellenlänge beim Photon auszurechnen, wendet an den Energieerhaltungssatz und den Impulserhaltungssatz auf das System Photon - Elektron an und erhält folgendes Ergebnis:

Für die Wellenlängenzunahme $\Delta \lambda$ des Röntgenphotons in Abhängigkeit von seiner Richtungsänderung, dem Streuwinkel, gilt:

$\begin{array}{l}\Delta \lambda =\lambda \text{'}-\lambda \\ \Delta \lambda =\frac{h}{m_{\text{e}}\cdot c}\cdot (1-\cos \beta )\\ \lambda \text{Wellenlänge vor der Streuung}\\ \lambda \text{'}\text{Wellenlänge nach der Streuung}\\ h\text{plancksches Wirkungsquantum}\\ m_{\text{e}}\text{Masse eines Elektrons}\\ c\text{Lichtgeschwindigkeit}\\ \beta \text{Winkel}\text{, um den das Photon aus seiner}\\ \text{ursprünglichen Richtung abgelenkt wird}\end{array}$

Die Konstante $\frac{h}{m_{\text{e}}\cdot c}$ bezeichnet man als COMPTON-Wellenlänge. Diese hat einen Wert von:

$\begin{array}{l}{\lambda }_{\text{C}}=\frac{h}{m_{\text{e}}\cdot c}\\ {\lambda }_{\text{C}}=\frac{\mathrm{6,626}\cdot \cdot {10}^{-34}\text{J}\cdot \text{s}}{\text{9}\text{,109}\cdot {10}^{\text{-31}}\text{kg}\cdot \mathrm{2,998}\cdot {10}^8\text{m}\cdot {\text{s}}^{\text{-1}}}\\ {\lambda }_{\text{C}}=\mathrm{2,426}\cdot {10}^{-12}\text{m}\\ \\ \text{Damit kann man für die Gleichung auch schreiben:}\\ \Delta \lambda ={\lambda }_{\text{C}}(1-\cos \beta )\end{array}$

Eine Interpretation dieser Gleichung ergibt:
Die Wellenlängenänderung ist unabhängig von der Frequenz des auftreffenden Photons. Deshalb macht sie sich bei kleinen Wellenlängen (hohen Frequenzen) prozentual am stärksten bemerkbar, z.B. bei Röntgenphotonen. Sie tritt aber auch bei Photonen anderer Frequenzen auf.

Herleitung der Gleichung für die Wellenlängenzunahme

Für den Stoß eines Photons gegen ein als ruhend angenommenes Elektron gelten der Energie- und der Impulserhaltungssatz der klassischen Mechanik.
Für die Energie gilt:
$h\cdot f_0=h\cdot f+\frac{1}{2}{m}_{\text{e}}\cdot v^2$
Für den Impuls gilt:
$\frac{h\cdot f_0}{c}=\frac{h\cdot f}{c}+m_e\cdot v$
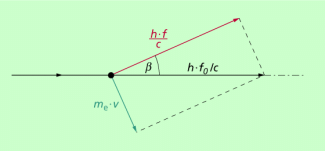
Ausgehend von Bild 2 erhält man für die Impulse unter Anwendung des Kosinussatzes den Ausdruck:
$\begin{array}{l}{(}^{m_e}={\left(\frac{h\cdot f_0}{c}\right)}^2+{\left(\frac{h\cdot f}{c}\right)}^2-2\frac{h\cdot f_0}{c}\cdot \frac{h\cdot f}{c}\cdot \cos \beta \\ {(}^{m_e}=\frac{h^2}{c^2}\left(f_0{}^2+f^2-2f_0\cdot f\cdot \cos \beta \right)\\ \text{Die Division durch}{m}_e\text{ergibt:}\\ m_e\cdot v^2=\frac{h^2}{m_e\cdot c^2}\left(f_0{}^2+f^2-2f_0\cdot f\cdot \cos \beta \right)\end{array}$

Setzt man den Ausdruck in den oben genannten Energieerhaltungssatz ein, so erhält man:
$\begin{array}{l}h\cdot f_0=h\cdot f+\frac{h^2}{2m_e\cdot c^2}\left(f_0{}^2+f^2-2f_0\cdot f\cdot \cos \beta \right)\\ \text{Aus dieser Gleichung folgt durch Umstellung für die}\\ \text{Frequenzänderung:}\\ f_0-f=\frac{h}{2m_e\cdot c^2}\left(f_0{}^2+f^2-2f_0\cdot f\cdot \cos \beta \right)\\ \text{Da für alle praktisch vorkommenden Fälle}{f}_0-f\ll f_0\text{ist}\text{,}\\ \text{kann man}{f}_0{}^2\approx f^2\approx f_0\cdot f\text{setzen}\text{. Damit erhält man:}\\ f_0-f=\frac{h\cdot f_0\cdot f}{2m_e\cdot c^2}\left(1+1-2\cos \beta \right)\text{oder vereinfacht:}\\ f_0-f=\frac{h\cdot f_0\cdot f}{m_e\cdot c^2}\left(1-\cos \beta \right)\end{array}$
In etwas anderer Schreibweise erhält man:
$\begin{array}{l}{f}_0-f=\frac{f_0\cdot f}{c}\cdot \frac{h}{m_e\cdot c}\left(1-\cos \beta \right)\text{oder nach Multiplikation}\\ \text{mit}\frac{c}{f_0\cdot f}:\\ \frac{f_0\cdot c}{f_0\cdot f}-\frac{f\cdot c}{f_0\cdot f}=\frac{h}{m_e\cdot c}\left(1-\cos \beta \right)\\ \text{Mit}\frac{c}{f}=\lambda \text{erhält man als Gleichung für die Zunahme der}\\ \text{Wellenlänge:}\\ \lambda -{\lambda }_{\text{0}}=\frac{h}{m_e\cdot c}\left(1-\cos \beta \right)\end{array}$