Längenkontraktion

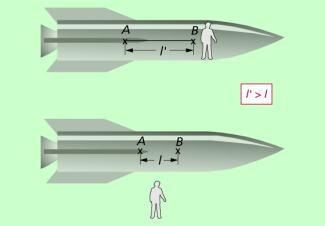
In der klassischen Physik hat die Länge eines Körpers und damit der Abstand zweier Punkte einen bestimmten, stets gleichen Wert. In der Relativitätstheorie dagegen zeigt sich, dass die Länge eines Körpers vom Bezugssystem abhängig ist (Bild1).

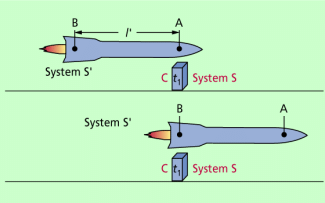
Als Beispiel betrachten wir dazu eine sehr schnell fliegende Rakete (Bild 2), die in den Punkten A und B zwei synchronisierte Lichtuhren mitführt. Die Rakete betrachten wir als Bezugssystem S'. Der Abstand zwischen A und B betrage l'. Das ist zugleich die Länge eines gegebenen Körpers im System S'. Die Rakete bewegt sich gegenüber einem System S, in dem sich eine Lichtuhr C befindet, mit der Geschwindigkeit v nach rechts.
Gemessen wird die Zeit des Vorbeifluges der Rakete an C von beiden Systemen aus.

Für das Bezugssystem S' ergibt sich:
$\begin{array}{l}\text{Die Zeit für den Vorbeiflug beträgt }\Delta t\text{'}.\text{ Damit ergibt sich}\\ \text{als Abstand bzw}\text{. Länge:}\\ \overline{AB}=l\text{'}=c\cdot \Delta t\text{'}\end{array}$

Für das Bezugssystem S ergibt sich aufgrund der Zeitdilatation:
$\begin{array}{l}\text{Die Zeit für den Vorbeiflug beträgt die kürzere Zeit }\Delta t.\\ \text{Damit ergibt sich der kleinere Abstand bzw}\text{. die kleinere Länge:}\\ \overline{AB}=l=c\cdot \Delta t\end{array}$

Allgemein gilt:
In seinem Ruhessystem hat ein Körper die größte Länge, die als Eigenlänge bezeichnet wird. In einem dazu bewegten System ist die Länge geringer.

Herleitung aus der Zeitdilatation
Der mathematische Zusammenhang ergibt sich aus der Gleichung für die Zeitdilatation. Sie lautet:
$\Delta t\text{'}=\frac{\Delta t}{\sqrt{1-v^2/c^2}}$
Stellt man die beiden oben genannten Gleichungen für die Längen (Abstände) l und l' nach den jeweiligen Zeiten um und setzt diese Zeiten in die Gleichung für die Zeitdilatation ein, so erhält man:
$\begin{array}{l}l\text{'}=\frac{l}{\sqrt{1-v^2/c^2}}\text{ oder umgestellt: }l=l\text{'}\cdot \sqrt{1-v^2/c^2}\\ \text{Mit dem LORENTZ-Faktor }k=\frac{1}{\sqrt{1-v^2/c^2}}\text{ kann man auch schreiben:}\\ l\text{'}=k\cdot l\text{ und }l=\frac{l\text{'}}{k}\end{array}$

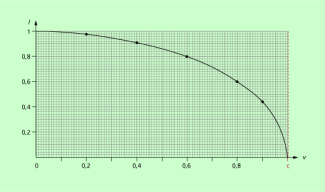
Die Veränderung der Länge mit dem LORENTZ-Faktor k ist grafisch in Bild 3 dargestellt. Bei kleiner Geschwindigkeit ist die Längenkontraktion vernachlässigbar klein. Die Länge des Körpers ist gleich seiner Eigenlänge. Bei der Lichtgeschwindigkeit c wäre die Länge null.

Herleitung aus der LORENTZ-Transformation

In seinem Ruhesystem S' hat der Körper die Länge:
$l\text{'}=x_2\text{'}-x_1\text{'}$
Im Bezugssystem S hat der gleiche Körper die Länge
$l=x_2-x_1$
Sie wird zu einem bestimmten Zeitpunkt durch die Bestimmung des Endpunktes und des Anfangspunktes des Körpers festgelegt. Es gilt also dann für die Zeiten in S:
$t_1=t_2\text{oder}\Delta t=0$
Eine Anwendung der LORENTZ-Transformation ergibt:
$\begin{array}{l}{x}_1\text{'}=\frac{x_1-v\cdot t_1}{\sqrt{1-v^2/c^2}}{x}_2\text{'}=\frac{x_2-v\cdot t_2}{\sqrt{1-v^2/c^2}}\\ \text{Damit erhält man als Länge:}\\ l\text{'}=x_2\text{'}-x_1\text{'}=\frac{(x_2-v\cdot t_2)-(x_1-v\cdot t_1)}{\sqrt{1-v^2/c^2}}\\ \text{Mit}{t}_1=t_2\text{bzw}\text{.}\Delta t=0\text{ergibt sich:}\\ l\text{'}=\frac{x_2-x_1}{\sqrt{1-v^2/c^2}}=\frac{l}{\sqrt{1-v^2/c^2}}\end{array}$