Zentraler gerader unelastischer Stoß

Kennzeichnung eines zentralen unelastischen Stoßes

Ein zentraler gerader unelastischer Stoß zwischen zwei Körpern ist dadurch gekennzeichnet, dass

• die Verbindungsgerade der Schwerpunkte beider Körper senkrecht auf der Berührungsfläche steht, die sich beim Stoß ausbildet (zentraler Stoß),
• beim Stoß keine elastischen Wechselwirkungen auftreten,
• sich die Körper nach dem Stoß mit einer gemeinsamen Geschwindigkeit weiterbewegen und
• ein Teil der mechanischen Energie in andere Energieformen umgewandelt wird.

Beispiele für Stöße, die näherungsweise als solche zentralen unelastischen Stöße angesehen werden können, sind der Zusammenstoß von Autos, der Aufprall eines Steines auf den Erdboden, der Einschlag einer Kugel in einen Körper oder der Schlag eines Hammers auf einen Nagel, der in Holz eingeschlagen wird. Unelastische Stöße treten auch bei Elementarteilchen auf.
Dabei ist aber stets zu beachten: Ein (ideal) unelastischer Stoß ist eine Idealisierung, die in der Praxis nur näherungsweise auftritt. Damit muss auch für den jeweiligen Fall geprüft werden, ob die nachfolgend genannten Gesetze angewendet werden können.

Gesetze für den zentralen unelastischen Stoß

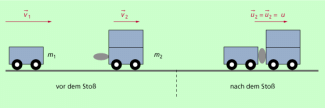
Wir betrachten als Beispiel einen zentralen unelastischen Stoß zwischen zwei Wagen (Bild 2). Beim Stoß kleben die beiden Wagen aneinander und fahren mit der gleichen Geschwindigkeit weiter. Die gesamte Anordnung betrachten wir als ein abgeschlossenes System, vernachlässigen damit auch den Einfluss von Reibuntgseffekten.
Für eine solche Anordnung gilt der Impulserhaltungssatz:

$\begin{array}{l}{m}_1\cdot {\overrightarrow{v}}_1+m_2\cdot {\overrightarrow{v}}_2=(m_1+m_2)\overrightarrow{u}\\ \text{Betrachten wir zur Vereinfachung nur die Beträge und}\\ \text{gehen wir von der gleichen Bewegungsrichtung aus (Bild 2)}\text{,}\\ \text{so vereinfacht sich die Gleichung zu:}\\ m_1\cdot v_1+m_2\cdot v_2=(m_1+m_2)u\\ \text{Die Umstellung nach }u\text{ ergibt:}\\ u=\frac{m_1\cdot v_1+m_2\cdot v_2}{m_1+m_2}\end{array}$
Eine unterschiedliche Bewegungsrichtung der einzelnen Körper muss durch unterschiedliches Vorzeichen berücksichtigt werden. Dabei ist es wie in der Mathematik üblich, eine Bewegung nach rechts als positive Richtung anzusehen. In welcher Richtung sich die Körper nach dem Stoß gemeinsam weiterbewegen, hängt von den Impulsen beider Körper vor dem Stoß ab. Die gemeinsame Bewegung erfolgt immer in der Richtung, die der größere Impuls hat.

Spezielle Fälle

Von Interesse sind vor allem zwei spezielle Fälle:
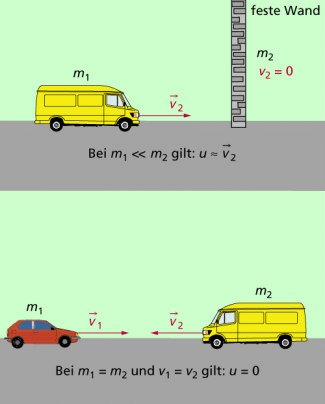
a) Einer der am Stoß beteiligten Körper hat eine wesentlich größere Masse als der andere (Stoß gegen eine feste Wand, Kollision eines Autos mit einen Baum). Dann gilt: Beide Körper bewegen sich näherungsweise mit der Geschwindigkeit des Körpers mit der größeren Masse weiter oder sind nach dem Stoß in Ruhe, wenn der schwere Körper (die feste Wand) vorher in Ruhe war (Bild 3a).
b) Beide Körper haben die gleiche Masse und den gleichen Betrag der Geschwindigkeit, aber sie bewegen sich vor dem Stoß aufeinander zu (Bild 3b). Dann sind beide Körper nach dem Stoß in Ruhe.

Energiebilanz beim zentralen unelastischen Stoß

Beim unelastischen Stoß gilt zwar der allgemeine Energieerhaltungssatz, nicht aber der Energieerhaltungssatz der Mechanik, da bei unelastischen Verformungen ein Teil der Energie in Verformungsenergie und in thermische Energie umgewandelt wird. Der auftretende „Verlust“ an mechanischer Energie ist ein Maß für die zerstörerische Wirkung des Stoßes.
Für die Energiebilanz bei einem solchen unelastischen Stoß gilt:

Die kinetische Gesamtenergie der Körper vor dem Stoß ist die Summe der kinetischen Energien der einzelnen Körper:

$E_{\text{kin}\text{, vor}}=\frac{1}{2}{m}_1\cdot v_1^2+\frac{1}{2}{m}_2\cdot v_2^2$

Nach dem Stoß haben beide Körper zusammen die kinetische Energie:

$E_{\text{kin}\text{, nach}}=\frac{1}{2}(m_1+m_2)u^2$

Damit ergibt sich für die Verringerung der kinetischen Energie:

$\begin{array}{l}\Delta E=E_{\text{kin}\text{, vor}}-E_{\text{kin}\text{, nach}}\\ \Delta E=\frac{1}{2}{m}_1\cdot v_1^2+\frac{1}{2}{m}_2\cdot v_2^2-\frac{1}{2}(m_1+m_2)u^2\\ \text{Setzt man für die gemeinsame Geschwindigkeit }u\text{ den }\\ \text{oben aus dem Impulserhaltungssatz gewonnenen Term}\\ \text{ein}\text{, so erhält man nach einer Reihe von Umformungen}\\ \text{die Gleichung:}\\ \Delta E=\frac{1}{2}\frac{m_1\cdot m_2}{m_1+m_2}{(}^{v_1}\end{array}$

Dabei gilt das Minuszeichen, wenn die Körper vor dem Stoß dieselbe Geschwindigkeitsrichtung hatten (Auffahrunfall), das Pluszeichen beim Frontalzusammenstoß. Bei sonst gleichen Bedingungen ist der Verlust an kinetischer Energie in diesem Fall größer. Bei einem Verkehrsunfall wird dieser Energiebetrag in „Deformationsenergie“ umgewandelt. Deshalb haben Frontalzusammenstöße eine so verheerende Wirkung!