Apollonios-Kreis

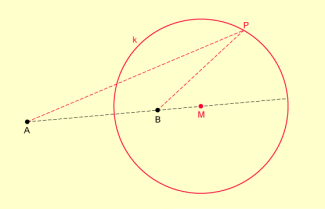
Der Nachweis, dass es sich bei der Menge der Punkte P(x; y) mit der gegebenen Eigenschaft tatsächlich um einen Kreis handelt, lässt sich mit den Mitteln der analytischen Geometrie relativ leicht führen.

O.B.d.A. nehmen wir dazu an, dass die Punkte A und B in einem ebenen kartesischen Koordinatensytem die Koordinaten (0; 0) bzw. (b; 0) haben.

Dann muss gelten:
$\sqrt{x^2+y^2}=2\cdot \sqrt{{(x-b)}^2+y^2}$
Durch Quadrieren und Umformen ergibt sich daraus
$x^2-\frac{8b}{3}x+y^2=-\frac{4}{3}{b}^2$
bzw. mittels quadratischer Ergänzung
${\left(x-\frac{4b}{3}\right)}^2+y^2=\frac{4}{9}{b}^2$.

Diese Gleichung beschreibt einen Kreis mit dem Mittelpunkt
$M\left(\frac{4b}{3};0\right)$und dem Radius $\frac{2}{3}b$.

In der obigen Abbildung ist der Sachverhalt dagestellt, wobei als feste Punkte die Punkte A(0; 0) und B(6; 0) gewählt wurden. Der APOLLONIOS-Kreis hat in diesem Fall den Mittelpunkt M(8; 0) und den Radius 4.

Die Punkte A, B, M und der Kreispunkt C sind sogenannte harmonische Punkte, d.h. Punkte der harmonischen Teilung der Strecke $\overline{AM}$, d.h., es gilt:
$\overline{MB}:\overline{BA}=\overline{MC}:\overline{CA}$

B ist der innere harmonische Teilpunkt, C der äußere harmonische Teilpunkt der Strecke $\overline{AM}$.