Das Computeralgebrasystem Derive

Das Computerprogramm Derive zählt zu den leistungstarken und auch bedienungsfreundlichen Computeralgebrasystemen (CAS). Es gehört deshalb zu den an Schulen mit am meisten genutzten CAS.

Anders als ein wissenschaftlicher Taschenrechner kann ein CAS wie Derive auch Terme mit Variablen umformen und vereinfachen (symbolische Termumformungen) sowie Gleichungen und Gleichungssysteme lösen. Zu den Fähigkeiten von Derive gehören auch zwei- und sogar dreidimensionale Abbildungen.

Der Derive-Bildschirm besteht aus der Titelleiste, der Menüleiste, der Befehlsleiste, dem Arbeitsfenster, der Statusleiste, der Eingabezeile und den Symbolleisten für griechische Buchstaben und mathematische Sonderzeichen.

Die Bedienung erfolgt über die Tastatur und über eine menügesteuerte Benutzeroberfläche: Meist gibt man einen Term oder eine Gleichung über die Tastatur in eine Eingabezeile ein und wendet einen Befehl an, der in der Menüleiste oder der Befehlsleiste ausgewählt und aktiviert wird.

Bild

Die Ausdrücke (Derive verwendet für alle Terme und Gleichungen gleichermaßen den Begriff Ausdruck) eines Arbeitsblattes werden zeilenweise nummeriert. Eingaben erscheinen links auf dem Arbeitsblatt, Ergebnisse werden standardmäßig zentriert dargestellt.

Beachte:
Bei Dezimalzahlen ist anstelle des Kommas immer ein Punkt einzugeben.
Für die Exponent-Schreibweise wird die ^-Taste verwendet; die Zeichen für $π u n d \sqrt$ findet man in der Symbolleiste für mathematische Sonderzeichen.

Standardmäßig arbeitet Derive im exakten Rechenmodus. Zahlen werden als Dezimalzahlen, gemeine Brüche oder durch entsprechende Symbole (z.B. $π, e$ ) dargestellt. Wird als Ergebnis einer Rechnung ein Näherungswert gewünscht, muss die Schaltfläche bzw. der Befehl Approximieren gewählt werden.

Bild

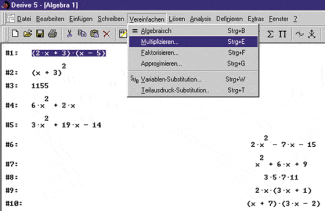
Termumformungen

Sollen Produkte ausmultipliziert oder Summen in Produkte umgeformt werden, verwendet man Befehle Ausmultiplizieren bzw. Faktorisieren des Menüs Vereinfachen.

Symbolische Termumformungen mit Derive

Sollen Variable eines Terms durch konkrete Werte ersetzt werden, kann die Schaltfläche Substitution oder der entsprechende Befehl im Menü Vereinfachen verwendet werden.

Bild

Beachte:
Insbesondere bei der Eingabe von Bruchtermen ist die Struktur des Terms genauestens zu berücksichtigen. Dazu sind des Öfteren Klammern zu setzen, auch wenn diese in der üblichen Schreibweise nicht vorhanden sind. Lässt man eine solche Klammer weg, erhält der Term eine andere Bedeutung. Die im Arbeitsfenster dargestellte Eingabe ist deshalb eine gute Kontrolle, ob der Term richtig eingegeben wurde.

Bild

Lösen von Gleichungen

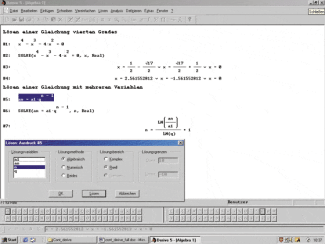
Zum Lösen von Gleichungen – auch mit mehreren Variablen – besitzt Derive den SOLVE-Befehl. Nach Eingabe der zu lösenden Gleichung wird die Schaltfläche Ausdruck lösen betätigt. Im sich öffnenden Dialogfeld Lösungsvariablen ist nun die Variable zu markieren, nach der aufgelöst werden soll. Die Schaltfläche Lösen führt den Befehl aus.

Lösen von Gleichungen

Differenziation und Integration von Funktionen

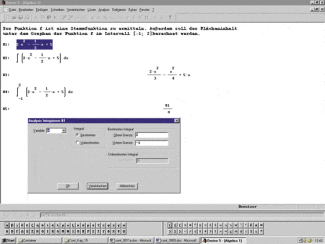
Für die Differenziation und Integration stellt Derive im Menü Analysis leicht handhabbare Untermenüs zur Verfügung.

Beispiel: Zur Funktion f mit $f (x) = 2 x^{2} - \frac{1}{2} x + 5$ ist eine Stammfunktion zu ermitteln. Außerdem soll der Flächeninhalt unter dem Graphen der Funktion f im Intervall [-1; 2] berechnet werden.

Ermitteln von unbestimmten und bestimmten Integralen

Grafische Darstellung von Funktionen

Die grafische Darstellung von Funktionen erfolgt im 2-D-Grafik-Fenster. Es wird mit der Schaltfläche oder dem Befehl Fenster/Neues 2D-Graphik-Fenster geöffnet. Für das weitere Arbeiten ist es praktisch, das Grafik-Fenster und das Algebra-Fenster nebeneinander anzuordnen.

Beispiel: Grafische Darstellung der Funktion $y = f (x) = x^{3} - e^{x}$

Grafische Darstellung einer Funktion

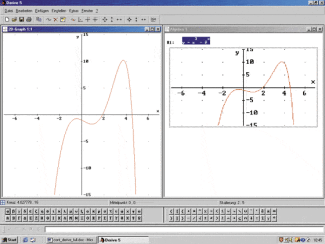
Die Funktionsgleichung wird über die Eingabezeile in das Algebra-Fenster eingetragen bzw. dort markiert.
Bei Verwendung der Ausdruck zeichnen-Schaltfläche wird der Funktionsgraph sofort in ein Koordinatensystem gezeichnet.
Die im Grafikfenster erzeugten und bearbeiteten grafischen Darstellungen können ausgedruckt, aber noch nicht gespeichert werden. Mithilfe des Befehls Einbetten im Menü Datei wird die Grafik in das Arbeitsblatt kopiert. Dieses Arbeitsblatt kann durch Texte ergänzt, ausgedruckt und auch gespeichert werden.

Darstellen einer Kurvenschar

Beispiel: Die Kurvenschar der Funktionen $f_{k} (x) = \frac{1}{6 k} x^{3} - x^{2} + \frac{3}{2} k x$ soll für $k = - 3; - 2; - 1; 0; 1; 2; 3$ gezeichnet werden.

Variante 1:
Für jeden Parameter k wird die zugehörige Funktionsgleichung aufgestellt. Werden alle Gleichungen markiert, so erfolgt die Darstellung der Funktionsgraphen in ein und demselben Koordinatensystem wie zu der vorangegangenen Abbildung erläutert.

Variante 2:
Schneller lässt sich die Kurvenschar mit dem Vektor-Befehl aus dem Analysis-Menü darstellen. Dieser Befehl erzeugt eine Liste mit Werten, die als Koeffizienten eingesetzt werden.

Darstellung einer Kurvenschar

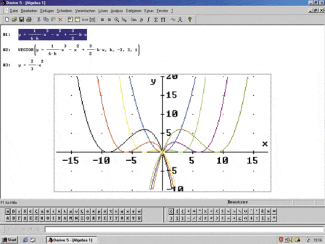
Zusätzlich kann auch noch eine Ortskurve – z.B. die der lokalen Hochpunkte – eingezeichnet werden. Ist deren Gleichung nicht bekannt, kann sie auch durch Experimentieren mit der vorzugebenden Gleichung ermittelt werden.

3-D-Darstellungen

Mithilfe des 3-D-Grafikfensters können auch Funktionen mit zwei Variablen grafisch dargestellt werden (3-D-Darstellung). Da jede derartige Funktion eine Fläche im dreidimensionalen Raum beschreibt, können insbesondere auch Ebenengleichungen (in Koordinatenschreibweise) veranschaulicht werden.

Als erstes trägt man die zu veranschaulichende(n) Gleichung(en) in das Algebrafenster ein und markiert sie. Dann wird über die Menü- oder Befehlsleiste das 3-D-Grafikfenster geöffnet. Über den Zeichnen-Befehl erfolgt sofort die Darstellung der Ebenen.

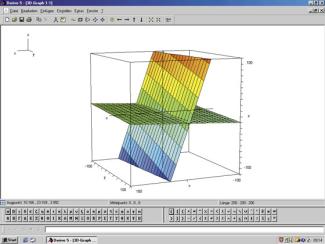
Beispiel: Die folgende Abbildung zeigt die Ebenen mit den folgenden Gleichungen:
$E_{1} : 11 x + y + 4 z - 29 = 0 u n d E_{2} : 3 x - 2 y - 58 z - 58 = 0$

3D-Darstellung: Schnitt zweier Ebenen

Experimentieren mit Zufallszahlen

Mithilfe eines integrierten Zufallszahlengenerators und des Befehls RANDOM(n) erzeugt Derive für $n > 1$ ganzzahlige Zufallszahlen von $0 b i s n - 1$ .
So erhält man beispielsweise mit RANDOM(2) Zufallszahlen 0 oder 1 und mit RANDOM(6) $Z u f a l l s z a h l e n 0, 1, 2, 3, 4 o d e r 5$ .
Das Werfen einer Münze (mit 1 für Zahl und 0 für Wappen) kann demzufolge durch RANDOM(2) und das Werfen eines Würfels durch $1 + R A N D O M (6)$ simuliert werden.

Anstelle die Random-Funktion 50-mal (oder öfter) nacheinander ausführen zu müssen, kann wieder die Vektorfunktion verwendet werden. Der VEKTOR-Befehl aktiviert den Zufallsgenerator mehrfach und stellt die Zufallszahlen als Liste dar. Auf diese Art können sehr schnell 100, 1000 oder mehr Würfe simuliert werden.

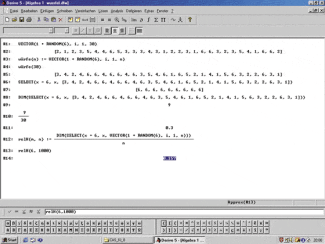
Beispiel: Die Aufgabenstellung Simuliere 30 Würfe mit einem Würfel und ermittle die relative Häufigkeit für das Auftreten einer „6" kann mit folgenden Arbeitsschritten gelöst werden:

1.	Man öffnet ein neues Arbeitsblatt und erzeugt eine Liste mit den Ergebnissen von 30 Würfen mit einem Würfel. Dazu tippt man folgenden Befehl in die Eingabezeile und führt den Befehl aus: VECTOR(1+RANDOM(6),i,1,30)	$(# 1, # 2)$
2.	Soll der Versuch mehrfach durchgeführt werden, ist es sinnvoll, eine spezielle Funktion würfe zu definieren. Den dazu erforderlichen Zuordnungsoperator erhält man mithilfe der Tasten. Man definiert würfe durch folgende Eingabe: $w ü r f e (n) : = V E C T O R (1 + R A N D O M (6), i, 1, n)$ Man simuliert jetzt noch einmal 30 Würfe. Dazu gibt man ein: würfe(30)	$(# 3, # 4, # 5)$
3.	Um zu ermitteln, wie oft die 6 „gewürfelt“ wurde, kann man den SELECT-Befehl für $x = 6$ auf Zeile $# 5$ anwenden: $S E L E C T (x = 6, x, # 5)$ Hinweis: Es werden alle in Zeile $# 5$ „gewürfelten“ Sechsen angezeigt.	$(# 6, # 7)$
4.	Gezählt und angegeben wird die Anzahl der in Zeile $# 5$ „gewürfelten“ Sechsen mit dem DIM-Befehl: $D I M S E L E C T (x = 6, x, # 5)$	$(# 8, # 9)$
5.	Als Letztes soll die relative Häufigkeit der geworfenen Sechsen berechnet werden. Dazu muss die Gleichung $r e l a t i v H ä u f i g k e i t = \frac{a b s o l u t e H ä u f i g k e i t}{A n z a h l d e r V e r s u c h e}$ angewandt werden. Für das hier demonstrierte Beispiel lautet die Eingabe: $# 9 / 30$ Hinweis: Hier sollte mit $\approx$ abgeschlossen werden.	$(# 10, # 11)$

Jetzt können die Arbeitsschritte 2 bis 5 für eine andere Anzahl von Würfen und auch für eine andere zu würfelnde Zahl wiederholt werden.

Simulationen mit einem Würfel

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Das Computeralgebrasystem Derive

Termumformungen

Lösen von Gleichungen

Differenziation und Integration von Funktionen

Grafische Darstellung von Funktionen

Darstellen einer Kurvenschar

3-D-Darstellungen

Experimentieren mit Zufallszahlen

Rechtliches

Einloggen