Deterministisches Chaos
Ordnung und Chaos
Mit den Begriffen „Ordnung“ und „Chaos“ verbinden Menschen seit jeher recht unterschiedliche Vorstellungen. Die Alltagsvorstellungen dazu könnte man vielleicht folgendermaßen zusammenfassen:
Ordnung bedeutet Wahrung der Tradition, die Beachtung der Gesetze und Normen. Sie ist verbunden mit Übersichtlichkeit, Klarheit, Vollkommenheit.
Chaos dagegen ist das Gegenteil von Ordnung, ein wildes Durcheinander, hervorgerufen durch Anarchie oder Katastrophen. Es ist verbunden mit dem ungewollten und unberechenbaren Zufällen.
Die Begriffe Ordnung und Chaos spielen nicht nur im Alltagsleben eine Rolle, sondern auch in den Naturwissenschaften, speziell in der Physik. Das Naturgeschehen ist für den Physiker „ordentlich“, wenn er es eindeutig beschreiben und das künftige Verhalten vorhersagen kann. Das ist ein zwei grundlegenden Voraussetzungen geknüpft:
- Objektivierbarkeit : Darunter versteht man die Überzeugung, das Vorgänge in der Natur unabhängig von unseren Vorstellungen und Wünschen verlaufen, also objektiv vor sich gehen.
- Kausalität : Darunter versteht man die Überzeugung, dass jeder Vorgang in der Natur durch ganz bestimmte Ursachen in gesetzmäßiger Weise bestimmt ist und dass gleiche Ursachen stets gleiche Wirkungen nach sich ziehen. Für viele Vorgänge in Natur und Technik lässt sich eine solche Kausalität als funktionaler Zusammenhang zwischen physikalischen Größen des betreffenden Systems finden, z. B.
| – | Beim Erwärmen eines Metallstabes vergrößert sich dessen Länge. Dafür gilt die Beziehung: Ändert sich die Temperatur um einen bestimmten Wert, kann man eindeutig vorhersagen, welche Längenänderung beim Metallstab vor sich geht. |
| – | Durch das Wirken einer Kraft wird ein Körper beschleunigt. Dabei gilt: Kennt man den Betrag der beschleunigenden Kraft und die Masse des Körpers, dann kann man die Beschleunigung eindeutig ermitteln. |
Die großen Erfolge der Physik im 18. und 19. Jahrhundert, insbesondere auch solche Leistungen wie die Berechnung von Planetenbahnen, verstärkten die Überzeugung von der Kausalität im Naturgeschehen. Zusammengafasst wurde diese Weltsicht im Jahr 1812 von dem französichen Mathematiker und Physiker PIERRE SIMON LAPLACE (1749-1827). Sie wird auch als laplacescher Dämon bezeichnet:
„Wir müssen also den gegenwärtigen Zustand des Weltalls als die Wirkung eines früheren und als die Ursache des folgenden Zustandes betrachten. Eine Intelligenz, welche für einen gegebenen Augenblick alle in der Natur wirkenden Kräfte sowie die genwärtige Lage der sie zusammensetzenden Elemente kennt und überdies umfassend genug wäre, um diese gegebenen Größen der Analyse zu unterwerfen, würde in derselben Formel die Bewegung der größten Weltkörper wie des leichtesten Atoms umschließen; nichts würde ihr ungewiss sein, und Zukunft wie Vergangenheit würden ihr offen vor Augen stehen.“
Diese enge, mechanistische Interpretation der Kausalität, die davon ausgeht, dass es Naturgesetze gibt, die den künftigen Zustand eines Systems eindeutig aus dem gegenwärtigen Zustand bestimmen, nennt man Determinismus (Bestimmtheit). Man kann das Prinzip des Determinismus auch folgendermaßen formulieren:
| Gleiche Ursachen haben gleiche Wirkungen. |
Oder abgeschwächt:
| Ähnliche Ursachen haben ähnliche Wirkungen. |
Gibt es nur eine Kausalität?
Einfache physikalische Erscheinungen wie die Ausdehnung eines Körpers bei Temperaturerhöhung oder die Brechung des Lichtes beim Übergang von einem Stoff in einen anderen sprechen für die Determiniertheit von Vorgängen. Es gibt allerdings auch Argumente dagegen:
| – | Untersuchungen in der Quantenphysik haben gezeigt, dass von Mikroobjekten nicht gleichzeitig Ort und Impuls beliebig genau bestimmt werden können. |
| – | Es ist auch mit modernsten Messgeräten nicht möglcih, Werte physikalischer Größen beliebig genau zu messen. Damit verbunden ist stets eine Unsicherheit, ob gleiche Ursachen tatsächlich gleiche Wirkungen hervorrufen. |
Beim Finden erster physikalisicher Gesetze war es allerdings von entscheidender Bedeutung, dass es eine Reihe von Vorgängen gibt, bei denen kleine Abweichungen in den Ursachen auch nur zu kleinen Abweichungen in den Wirkungen führen. Ein Beispiel dafür ist die Entdeckung der Fallgesetze durch GALILEO GALILEI. Man bezeichnet solche Zusammenhänge als starke Kausalität .
Geringe Abweichungen in den Ausgangsbedingungen (Ursachen) können aber auch zu erheblichen Veränderungen in den Wirkungen führen. Man bezeichnet das als schwache Kausalität. In Bild 1 sind starke und schwache Kausalität gegenübergestellt und an einfachen Beispielen erläutert.
Physikalische Systeme, bei denen kleine Änderungen in den Anfangsbedingungen große Änderungen in den Auswirkungen haben können, bei denen also schwache Kausalität vorliegt, zeigen ein zufälliges oder chaotisches Verhalten. Da aber auch für solche Systeme die physikalischen Gesetzen gültig sind, bezeichnet man als solches Verhalten als deterministisches Chaos. Ein solches Verhaltes zeigen nicht nur viele physikalische Systeme, sondern auch chemische oder biologische Systeme. Einige Beispiele sind in Bild 1 genannt.
Ziel der Chaosforschung ist es,
| – | die Bedingungen zu bestimmen, unter denen sich Systeme chaotisch verhalten, |
| – | Gesetze zu finden, die das chaotische Verhalten solcher Systeme beschreiben, |
| – | festzustellen, durch welche Gesetze der Übergang von geordneten zu chaotischen Strukturen und Vorgängen beschrieben wird. |
Übersicht über starke und schwache Kausalität
Deterministisches Chaos - Kausalitäten
Sybille Storch, Berlin
Beschreibung chaotischer Systeme
Relativ einfach und überschaubar ist das Verhalten chaotischer mechanischer Systeme. Ein solches System ist ein Magnetpendel. Wird es in der Nähe eines Magneten gestartet, so wird es relativ schnell bei diesem Magneten zur Ruhe kommen. Wird das Pendel dagegen stark ausgelenkt und dann losgelassen, dann ist nicht vorhersagbar, wie es sich bewegt und bei welchem der drei Magnete ist schließlich stehen bleibt. Weitere Beispiele für einfache mechanische Systeme, die sich chaotisch verhalten, sind in der nachfolgenden Übersicht dargestellt.
Analysiert man die Vorgänge bei den drei genannten Systemen Magnetpendel, Doppelpendel und Doppelmulde, dann ergeben sich einige Gemeinsamkeiten, die auch für andere chaotische Systeme kennzeichnend sind:
- Die Systeme haben eine oder mehrere stabile Ausgangslagen. Das bedeutet: Bei kleinen Schwankungen um diese Lagen kann das System wieder in den ursprünglichen Zustand zurückkehren. Das ist in der Regel ein Zustand minimaler potenzieller Energie.
- Überschreiten die Schwankungen einen kritischen Wert, dann zeigen die Systeme ein nicht mehr vorhersagbares Verhalten. Dabei reagiert das System sehr sensibel auf kleine Änderungen der Anfangsbedingungen.
Ursache für diese Sensibilität ist das Vorhandensein von Zuständen, in denen die potenzielle Energie maximal wird. Hat ein System ungefähr diese Energie, dann entscheidet ein winziger Energiebetrag beim Erreichen dieses Zustandes, ob das System
| – | seinen Weg über den „Berg potenzieller Energie“ fortsetzen wird, |
| – | kurz vor dem Gipfel des Potenzialberges umkehren wird oder |
| – | auf dem Potenzialberg zum Stillstand kommt. |
Befindet sich das System gerade auf einem solchen Potenzialberg, so ist sein Verlassen in jeder Richtung möglich - sein Verhalten ist symmetrisch. Nähert sich aber ein chaotisches System in der beschriebenen Weise der „Bergspitze“, so sind die Richtungen der weiteren Entwicklung nicht mehr gleichberechtigt. Die Symmetrie ist gebrochen.
Ein einfaches Magnetpendel verhält sich chaotisch.
Deterministisches Chaos - Magnetpendel
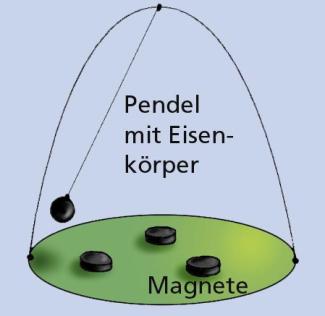
Sybille Storch, Berlin
Betrachtet man das Verhalten chaotischer Systeme in der Nähe eines Potenzialberges genauer, so werden zwei weitere Merkmale solcher Systeme deutlich:
(3) Wird ein chaotisches System, das sich im Zustand maximaler potenzieller Energie befindet, geringfügig ausgelenkt, so kehrt es nicht in die Ausgangslage zurück, sondern die Auslenkung wird immer größer. Sie verstärkt sich selbst. Diese Selbstverstärkung nennt man auch positive Rückkopplung.
(4) Die Kräfte, die das System veranlassen, sich immer schneller vom Potenzialberg zu entfernen, hängen nicht linear von der Auslenkung ab. Es gilt:
Man kann die Sinusfunktion auch als unendliche Reihe schreiben:
Wenn das Fadenpendel aus der unteren Gleichgewichtslage um einen kleinen Winkel ausgelenkt wird, dann können die höheren Potenzen von x vernachlässigt werden (bei einem Winkel kleiner als 5° ist x > 0,0873). Es gilt dann in guter Näherung ein lineares Kraftgesetz. Das führt zu der bekannten Gleichung für eine harmonische Schwingung. Bei größeren Auslenkungen oder bei einem Fadenpendel, das aus einer oberen Gleichgewichtslage ausgelenkt wird, können die größeren Potenzen von x nicht mehr vernachlässigt werden. Daraus kann man verallgemeinern: Ein charakteristisches Merkmal von chaotischen Systemen ist die Beschreibung durch nichtlineare Gleichungen.
Beschreibung chaotischer Systeme
Zur Beschreibung des Verhaltens chaotischer Systeme ist es oft nicht notwendig, die Vorgänge vom Beginn bis zum Ende der Beobachtung genau nachzuvollziehen. Es reicht häufig zu wissen, von welchem Startpunkt (Ursache) welcher Endpunkt (Wirkung) erreicht wird. Da chaotische Systeme von diesen Endpunkten gewissermaßen „angezogen“ werden, nennt man sie auch Attraktoren. Durch die grafische Darstellung solcher Akktraktoren kann die Sensibilität chaotischer Systeme gegenüber den Anfangsbedingungen genauer erfasst werden. Wir betrachten dazu nachfolgend einige Beispiele.
Magnetpendel : Für ein Magnetpendel kann man für die unterschiedlichsten Startpunkte erfassen, bei welchem Magneten das Pendel letztendlich stehen bleibt. Verfolgt man die Bewegungen, so erhält man Attraktoren, so wie sie in Bild 3 dargestellt sind.
Entwicklung von Tierpopulationen : Schon 1845 stellte der belgische Mathematiker P. F. VERHULST bei der Entwicklung von Tierpopulationen ein chaotisches Verhalten fest. Zur Beschreibung der Größe einer Tierpopulation hat er eine Gleichung entwickelt: Wenn r eine für die betrachtete Tierpopulation typische Vermehrungsrate ist, so ergibt sich die Anzahl der nächsten Generation
Zum besseren Vergleich verschiedener Populationen wird dabei x zwischen 0 und 1 normiert, d.h. x = 1 bedeutet 100 % der möglichen Anzahl von Tieren einer bestimmten Art. Damit würde aber exponenzielles Wachstum vorliegen und die Tierpopulation würde sehr schnell ins Unermessliche wachsen. Ein solches ungehemmtes Wachstum wird aber z. B. durch das vorhandene Territorium und durch das begrenzte Nahrungsangebot gehemmt. Das hat VERHULST in seiner Gleichung durch einen Faktor berücksichtigt. Je mehr Tiere in der vorangegangenen Generation vorhanden waren und sich gegenseitig Konkurrenz machen, umso weniger Tiere werden in der darauf folgenden Generation überleben. Man erhält damit die sogenannte logistische Gleichung. Das ist eine nichtlineare Gleichung, wie sie typisch für die Beschreibung chaotischer Vorgänge ist. Sie lautet:
Attraktoren für ein Magnetpendel mit drei Magneten. Die drei Attraktoren sind rot, blau und gelb eingefärbt.
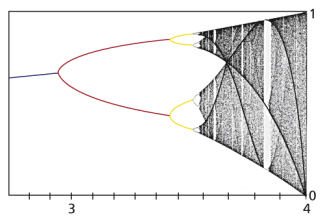
Die Sensibilität gegenüber den Anfangsbedingungen kann man mathematisch untersuchen. Das ist erst in den letzten Jahrzehnten gemacht worden, weil dazu eine leistungsfähige Rechentechnik erforderlich ist. Entscheidenden Anteil daran hatte der amerikanische Physiker FEIGENBAUM (*1945), der 1975 erstmals entsprechende Diagramme angab, die man heute als FEIGENBAUM-Diagramme bezeichnet (Bild 4). Einem solchen Diagramm bzw. den zugrunde liegenden Berechnungen kann man u. a. folgende Informationen entnehmen
- Je nach dem Wert für r, der auf der Abszissenachse aufgetragen ist, ergeben sich völlig unterschiedliche Wirkungen: Bei r < 3 ist ein Attraktorwert vorhanden. Bei Vergrößerung von r schankt das System zunächst zwischen zwei Werten, mit weiterer Vergrößerung von r zwischen 4, 8, 16, 32 usw. Bei r > 3,57 verhält sich das System chaotisch, d. h. es ist nicht mehr vorhersagbar, welchen Wert das System anstrebt. Diese Aufspaltung der Linie in 2, 4, 8 usw. - in der Chaostheorie spricht man von Bifurkation - ist eine für viele chaotische Prozesse typische Periodenverdopplung. Betrachtet man z. B. die Stellen im Diagramm genauer, an denen sich eine Teilung vollzieht, so stellt man Muster fest, die sich immer kleiner werdend wiederholen. Berühmt ist in diesem Zusammenhang das sogenannten Apfelmännchen. Diese Selbstähnlichkeit ist ebenfalls typisch für chaotische Prozesse.
- In den das chaotische Verhalten charakterisierenden Bereichen fallen dunkle parabelförmige Linien auf. Längs dieser Linien besteht eine höhere Wahrscheinlichkeit für das Eintreten dieses Systemverhaltens.
- Inmitten der chaotischen Bereiche gibt es senkrechte weiße Bänder. In diesen „Fenstern der Ordnung“ wird das System stabil, das Verhalten wird wieder vorhersagbar.
FEIGENBAUM-Diagramm
Deterministisches Chaos - Feigenbaum-Diagramm
Ingo Berg
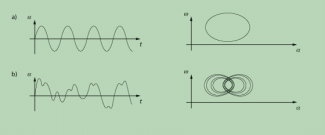
Wenn einem System nur einmal Energie zugeführt wird, dann lässt sich mit den beschriebenen Verfahren sein Verhalten hinsichtlich der Anfangsbedingungen beschreiben. Wird aber einem System ständig Energie zugeführt, dann hängt sein Verhalten nicht nur von den Anfangsbedingungen, sondern auch vom Rhythmus der Energiezufuhr ab. Das kann man z. B. experimentell mit einem Drehpendel demonstrieren. Zur Beschreibung ist es dann notwendig, den Zustand des Systems zu jedem Zeitpunkt zu erfassen. Das kann man bei einem Drehpendel über ein übliches Auslenkungs-Zeit-Diagramm (y-t-Diagramm) machen. Möglich ist aber auch ein sogenanntes Phasenraum-Diagramm. Dazu könnte man bei einem Drehpendel für jeden Zeitpunkt des Auslenkungswinkels und die Winkelgeschwindigkeit abtragen. Bild 5 zeigt die beiden Diagramme für verschiedene Dämpfung.
Phasenraum-Diagramme lassen gut erkennen, ob sich ein System periodisch verhält (geschlossener Kurvenzug) oder ob es chaotisches Verhalten zeigt.
Nachfolgend sind einige weitere Beispiele für Systeme dargestellt, die sich chaotisch verhalten können.
y-t-Diagramme und Phasenraum-Diagramme für ein Drehpendel bei verschiedener Dämpfung
Laminare und turbulente Strömungen
Strömungen von Flüssigkeiten oder Gasen können laminar und turbulent sein (Bild 6). Eine turbulente Strömung ist im Unterschied zu einer laminaren Strömung dadurch gekennzeichnet, dass Wirbel auftreten. Ob eine Strömung laminar oder turbulent erfolgt, hängt maßgeblich von der reynoldschen Zahl ab. Das ist eine Zahl, die nach dem englischen Physiker OSBORNE REYNOLDS (1842-1912) benannt ist und die von ihren Charakter her eine Ähnlichkeitszahl ist: Körper zeigen in Strömungen gleiches Verhalten, wenn ihre REYNOLDS-Zahl übereinstimmt. Berechnet werden kann diese Zahl mit der Gleichung
Für lange, gerade Rohre ergeben sich folgende Fälle:
| REYNOLDS-Zahl | Verhalten einer Flüssigkeit |
< 2 000 | Die Flüssigkeit strömt im Rohr laminar. |
| 2 000 - 3 000 | Die Strömung ist instabil und wechselt zwischen laminar und turbulent. |
| > 3 000 | Die Flüssigkeit strömt im Rohr turbulent. |
Berechnet man z. B. die REYNOLDS-Zahl für eine blutdurchströmte Kapillare im menschlichen Körper, dann erhält man mit
Das bedeutet: Blut fließt in unserem Körper laminar durch die Gefäße.
Grenzen der Wettervorhersage
Wetterdaten werden von zahlreichen Wetterstationen ständig gemessen. Erfasst werden dabei solche Daten wie Luftdruck, Temperatur, Windstärke und Regenmenge. Hinzu kommen Mess- und Beobachtungsergebnisse durch Wetterballons, Radaranlagen und Wettersatelliten. Die Vielzahl von aktuellen Daten ermöglicht in Verbindung mit moderner Rechentechnik relativ sichere Prognosen. Sie werden umso unsicherer, je länger der Prognosezeitraum ist und je kleiner der Bereich ist, auf den man die Prognose bezieht. Die Qualität von Wetterprognosen hängt auch von den verwendeten Modellen ab. Bei der Konstruktion solcher Modelle, wie sie z. B. der Deutsche Wetterdienst verwendet, wird die gesamte Erde mit einem Gittter aus vielen Punkten überzogen, die in verschiedenen Höhenschichten übereinanderliegen.
Das globale Modell spannt ein Gitter von 200 km Maschenweite über den Globus. Es ermöglichst Prognosen von bis zu sieben Tagen.
Das Europamodell verwendet 55 km auseinanderliegende Gitterpunkte und erfasst Europa, den Mittelmeerraum, Nordafrika und den Nordatlantik. Es liefert Wettervorhersagen für 3 Tage. Das Deutschlandmodell beschränkt sich auf Deutschland und seine Nachbarländer und besitzt eine räumliche Auflösung von 14 km. Seine Prognosen reichen bis 48 Stunden in die Zukunft.
Trotz des riesigen Aufwandes, der zur Sammlung von Wetterdaten und ihrer Auswertung betrieben wird, haben Prognosen für den nächsten Tag nur eine Trefferquote von 85 % bis 90 %. Bei einer Wettervorhersage für fünf Tage sinkt sie schon auf 65 %. Das Wetter für die nächsten 14 Tage ist praktisch nicht vorhersagbar. Die Ursachen dafür liegen nicht in der Qualität der Prognose begündet, sondern darin, dass Wetter ein chaotischer Prozess ist und sich damit einer exakten Vorhersage prinzipiell entzieht.
Der amerikanische Meteorologe E. N. LORENZ war einer der Ersten, der dies 1963 bemerkte, als er mit einem System aus drei Gleichungen ein Wettermodell berechnen wollte. Nachdem er seinem Computer die Messdaten eingegeben hatte, überbrückte er die Wartezeit in der Kantine. Beim Zurückkommen schaute er etwas misstrauisch auf das unerwartete Ergebnis (die Rechentechnik war damals nicht nur recht langsam, sondern nicht selten auch fehlerhaft) und gab ein Zwischenergebnis zur erneuten Berechnung ein. Diesmal errechnete der Computer eine völlig andere Vorhersage. Eine nochmalige Berechnung bestätigte: Es lag nicht am Computer. LORENZ hatte statt des genauen Zwischenergebnisse von 0,506127 den gerundeten Wert 0,506 eingegeben. Die Schlussfolgerung war: Offensichtlich können minimale Änderungen in den Anfangsbedingungen (z. B. Druck, Temperatur, Bewölkungsgrad) zu völlig unterschiedlichen Wetterentwicklungen führen.
In einer Vorlesung über seine Entdeckung fasste LORENZ diese Erscheinung in folgendes Bild:
„Der Flügelschlag eines Schmetterlings in Brasilien könnte einen Tornado in Texas verursachen.“
Die Strömung um ein Fahrzeug ist bei kleiner Relativgeschwindigkeit laminar, bei größerer Relativgeschwindigkeit treten Turbulenzen auf.
Das menschliche Herz - ein chaotisches System?
Das gesunde menschliche Herz schlägt bei normaler Belastung 60-80-mal in jeder Minute. Der Herzrhythmus wird aber mitunter durch zusätzliche Kontraktion oder „Aussetzer“ (Extrasystolen) gestört. Im Extremfall kann auch ein völlig unrythmischer Zustand, ein Herzkammerflimmern, eintreten. Ein solcher Zustand führt innerhalb kürzester Zeit zum plötzlichen Herztod. Ein im Vorfeld aufgenommenes EKG gibt nicht selten keinerlei Hinweise auf eine solche dramatische Entwicklung.
Da sowohl ein gesundes als auch ein krankes Herz mitunter unregelmäßig schlägt, wurde versucht, mit geeigneten Phasenraum-Diagrammen charakteristische Unterschiede zu erfassen. Dazu wurden die Zeitdifferenzen zwischen dem ersten und zweiten Herzschlag, dem zweiten und dritten und dem dritten und vierten gemessen und in einem räumlichen Koordinatensystem dargestellt. Die entsprechenden Zeitdifferenzen sind
Charakteristisch für ein gesundes Herz ist die eingegrenzte Keulenform. Bei gestörtem Herzrhythmus ist die Keulenform nicht mehr so ausgeprägt. Dagegen ist eine typische Wolke um die Keule zu erkennen, die durch die zeitweiligen „Stolperer“ hervorgerufen wird. Bei Herzkammerflimmern erscheint durch den sehr unregelmäßigen Herzschlag ein fast zufällig verteiltes Punktemuster.
Ein Angebot von 