- Lexikon
- Physik Abitur
- 6 Quantenphysik
- 6.2 Interferenz von Quantenobjekten
- 6.2.0 Interferenz von Quantenobjekten
- Interferenz bei Quantenobjekten
Interferenz bei Quantenobjekten
Solche Quantenobjekte kann man teilweise als Teilchen betrachten. Man kann z.B. Elektronen zählen. Sie fließen wie sehr kleine Kügelchen im elektrischen Leiter. Wir können ihre Bahn in einem Fadenstrahlrohr verfolgen. Trotzdem kann das Verhalten von Quantenobjekten in der Regel nicht vorhergesagt werden.
Interferenz mit Licht und mit Elektronen
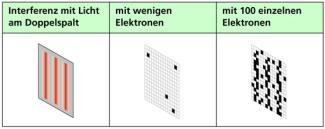
Interferenz am Doppelspalt
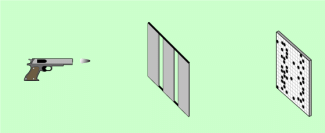
Das wird besonders deutlich, wenn man das Verhalten makroskopischer Objekte mit denen von Quantenobjekten vergleicht (Bild 2). Wenn man hinreichend häufig mit einer Pistole durch einen Doppelspalt feuert, erwartet man eine Verteilung, wie sie in Bild 2 dargestellt ist. Führt man aber analoge Versuche mit Elektronen oder anderen Quantenobjekten durch, dann erhält man eine Verteilung, wie man sie aus Interferenzversuchen mit Licht kennt (Bild 1). Alle diesbezüglichen Untersuchungen mit Quantenobjekten haben ergeben:
Bei Quantenobjekten kann Interferenz auftreten. Solche Interferenzen sind im Teilchenmodell nicht beschreibbar. Zur Interferenz von Elektronen sind unter dem Stichwort „Elektronenbeugung“ genauere Informationen auf der CD zu finden.
Verteilung von Geschossen hinter einem Doppelspalt
Interferenz am Einzelspalt
Wenn man Quantenobjekte durch einen Einzelspalt schickt, beobachtet man ein Interferenzmuster.
Je breiter der Spalt, umso dichter ist das Interferenzmuster. Wenn der Spalt extrem eng ist, bekommt man ein Interferenzmuster, das für alle x praktisch die gleiche Intensität hat.
Für jede der gedachten Möglichkeiten wird ein Zeiger ermittelt. Wenn wir uns 10 Punkte im Spalt denken, über die das Quantenobjekt den Punkt x erreichen könnte, erhalten wir 10 Zeiger, die addiert werden müssen. Tatsächlich sind es natürlich sehr viele (unendlich viele) Punkte, die man berücksichtigen muss. Um diese noch zeichnen zu können, wird die Länge der Zeiger entsprechend verkleinert. So bekommt man eine Schlange von unendlich vielen Punkten.
Die Beschreibung des Interferenzmusters kann mit der Zeigerschlange erfolgen. Je weiter der Detektionsort x von der optischen Achse entfernt ist, umso größer ist der Gangunterschied zwischen erstem und letztem Zeiger der Zeigerschlange. So ergeben sich die verschieden stark aufgerollten Zeiger in der Abbildung. Die Quadrate der Summenzeiger reproduzieren dann das beobachtete Interferenzmuster.
Für die Zeigerschlange für einen engeren Spalt gilt: Wenn der Spalt nur halb so breit ist, so ist auch die Zeigerschlange nur halb so gekrümmt. Dementsprechend ist das Interferenzmuster auch weiter gedehnt.
Fullerenenbeugung
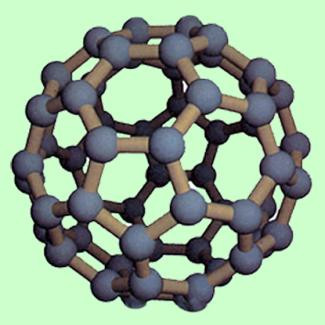
Fullerene sind Kohlenstoffmoleküle mit Fußballstruktur (Bild 3). Nach der Quantentheorie sollten alle Körper Interferenzeffekte zeigen, wenn sie nicht zu viele Freiheitsgrade haben und gut von der Umgebung isoliert sind. Verglichen mit einem Elektron ist ein Fulleren bereits ein sehr großes und komplexes System mit vielen Freiheitsgraden. Sein Durchmesser beträgt etwa 1 nm. Fullerenmoleküle bestehen aus 60 oder 70 Kohlenstoffatomen. Sie wurden 1987 bei Untersuchungen zum Aufbau der interstellaren Materie entdeckt.
Um den räumlichen Aufbau besser zu sehen, stellt man die Atome durch Punkte und die Bindungen durch Linien dar. Man erhält so ein Gebilde, das wie ein Fußball aussieht. Deshalb nennt man die Fullerene gelegentlich auch „Fußball-Moleküle“. Sie sind innen hohl. Wenn bei ihrer Entstehung Metallatome in der Nähe sind, wird jeweils eines davon in ihrem Inneren eingelagert.
Anwendungen von Fullerenen erhofft man sich in Medizin und Technik (z.B. in der Aidsforschung, in der Supraleitungs- und Nanotechnologie).
Schematische Zeichnung eines Fullerenmoleküls
Auf dem Interferenzbild ist nach oben die Anzahl der nachgewiesenen Atome aufgetragen. Erst wenn man eine größere Anzahl von Atomen bei verschiedenen Detektorpositionen nachgewiesen hat, ergibt sich das Muster. Man sieht dennoch immer noch die statistischen Abweichungen aufgrund des statistischen Verhaltens der Quantenobjekte.
Ein Angebot von 