- Lexikon
- Physik Abitur
- 6 Quantenphysik
- 6.3 Komplementarität und Unbetimmtheit
- 6.3.1 Komplementarität bei Doppelspalt-Experimenten
- Quantitative Beschreibung der Komplementarität
Quantitative Beschreibung der Komplementarität
Wahrscheinlichkeit und Zeigermodell
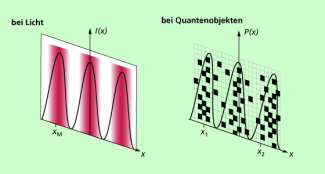
Die Funktion P(x) für Quantenobjekte hat den gleichen Verlauf wie die Funktion I(x), also der Verlauf der Intensität, bei Licht (Bild 1).
Intensität I(x) bei Licht und Wahrscheinlichkeit P(x) bei Quantenobjekten
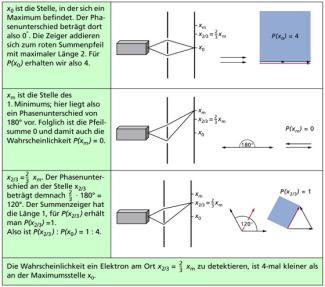
Für die Zeigerdarstellung ist allerdings zu beachten: Im Zeigermodell ist in der Optik das Quadrat des Summenzeigers ein Maß für die Intensität I für den betreffenden Ort x, bei Quantenobjekten ist es ein Maß für die Wahrscheinlichkeit P am Ort x. In Bild 2 ist als Beispiel dargestellt, welche Ergebnisse man erhalten würde, wenn man untersucht, mit welcher Wahrscheinlichkeit ein Elektron hinter einem Doppelspalt an bestimmten Stellen zu detektieren ist.
Wahrscheinlichkeit, ein Elektron an einer bestimmten Stelle zu detektieren
Die Komplementarität quantitativ
Wenn bei einem Quantenexperiment ein Interferenzmuster beobachtet wird, gibt es stets mehrere klassisch denkbare Möglichkeiten, wie ein Versuchsergebnis eintreten kann. Geht man vom Durchgang durch einen Doppelspalt aus, dann könnte das Quantenobjekt in klassischer Vorstellung durch den einen oder den anderen Spalt zu einem Ort x gelangen. Tatsächlich ist jedoch unbestimmt, durch welchen Spalt es geht. Führt man eine Messung an den Spalten durch, so erhält man nicht das Interferenzmuster, sondern die Summe der Einzelspaltverteilungen.
Um mithilfe der Zeiger die richtige Voraussage für die Wahrscheinlichkeit P(x) zu bekommen, müssen wieder die Zeiger zu den klassisch denkbaren Möglichkeiten gebildet werden. Beim Doppelspalt ist das ein Zeiger für die Möglichkeit „linker Spalt“ und ein Zeiger für die Möglichkeit „rechter Spalt“. Für ihre Addition gilt die Regel:
Zeiger dürfen n nicht vektoriell addiert werden, wenn sie zu Möglichkeiten gehören, die durch eine Messung unterscheidbar sind. Wenn die Möglichkeiten dagegen nicht durch eine Messung unterscheidbar sind, müssen die zugehörigen Zeiger vektoriell addiert werden.
Damit ergibt sich für Quantenobjekte folgende Abwandlung des Zeigermodells: Man muss jeweils diejenigen Zeiger vektoriell miteinander addieren, die zu Möglichkeiten gehören, welche nicht durch Messungen unterscheidbar sind. Die Zeigersummen werden quadriert. Die Summe der Quadrate ergibt die Wahrscheinlichkeit P(x).
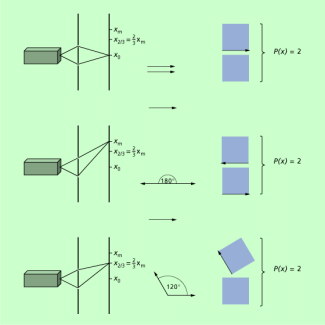
Beim Doppelspaltexperiment mit Ortsmessung an den Spalten erhält man bei diesem Herangehen für alle x die Summe zweier Einheitsquadrate, also P(x) = 2 (Bild 3). Das ist genau die richtige Verteilung bei kleiner Spaltbreite.
Wahrscheinlichkeit P(x) an verschiedenen Orten x
Zeigerdarstellung Doppelspaltexperiment Interferenzmuster Quantenobjekte Komplementarität Wahrscheinlichkeit Zeigermodell
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 