Zustandsgrößen der Sonne
Die Sonne ist der uns nächste Stern und zugleich das Massezentrum unseres Planetensystems. Das Gesamtbild unseres Zentralgestirns wird durch die physikalischen Zustandsgrößen Durchmesser (Radius), mittlere Dichte, Masse, Rotationsdauer, Leuchtkraft und Oberflächentemperatur bestimmt.
Nachfolgend werden die einzelnen Zustandsgrößen der Sonne näher charakterisiert.
Der Durchmesser der Sonne
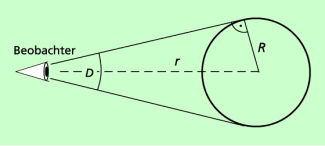
Aus der Beobachtung von totalen und ringförmigen Sonnenfinsternissen ergibt sich, dass sich der Winkeldurchmesser der Sonne, von der Erde aus gemessen, nur geringfügig ändert. Das hängt mit unterschiedlichen Entfernungen zwischen Erde und Sonne zusammen. Kennt man den Winkeldurchmesser und die Entfernung zwischen Erde und Sonne, dann kann man den Durchmesser bzw. den Radius der Sonne mithilfe einfacher geometrischer Überlegungen berechnen (Bild 2). Für den wahren Radius R unseres Zentralgestirns gilt:
Messungen der Entfernung zwischen Erde und Sonne haben eine mittlere Entfernung von 149,6 Mio. Kilometer (eine astronomische Einheit, 1 AE) ergeben. Der Winkeldurchmesser beträgt für diese mittlere Entfernung
D = 1919,3'' = 32'
Damit ergibt sich für den Radius der Sonne ein Wert von:
R = 696 000 km
Das entspricht dem 109fachen des Erdradius.
Aus dem scheinbaren Durchmesser der Sonne und ihrer Entfernung kann man ihren Durchmesser ermitteln.
Die Masse und die mittlere Dichte der Sonne
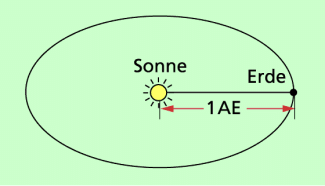
Die Masse der Sonne kann aus den Bahndaten der Planeten ermittelt werden. Zu der für die Berechnung erforderlichen Gleichung gelangt man durch folgende Überlegung (Bild 3):
Damit ein Planet auf einer kreisförmig gedachten Umlaufbahn um die Sonne gehalten wird, muss eine Radialkraft wirken. Diese Radialkraft ist die Gravitationskraft zwischen Sonne und Planet. Also gilt:
Setzt man die Gravitationskonstante G, die mittlere Entfernung Sonne-Erde r und die Umlaufzeit T der Erde in die Gleichung ein, so erhält man als Masse der Sonne einen Wert von:
Dieser Wert entspricht etwa dem 330 000fachen der Erdmasse.
Die mittlere Dichte der Sonne ergibt sich aus der allgemeinen Gleichung für die Dichte zu:
Setzt man die Daten der Sonne ein, so erhält man für ihre mittlere Dichte einen Wert von
Die mittlere Dichte der Sonne ist größer als die Dichte von Wasser und beträgt etwa ein Viertel der mittleren Dichte der Erde.
Die Rotationsdauer der Sonne
Aus der Beobachtung von Sonnenflecken ergibt sich, die diese von Ost nach West wandern, die Sonne also um eine Achse rotiert, die ungefähr senkrecht zu unserer Blickrichtung steht. Genauere Untersuchungen zeigen: Die Äquatorebene der Sonne ist um 7° 15' gegen die Ekliptik geneigt. Der Drehsinn der Sonne ist derselbe wie der Umlaufsinn der Planeten um sie, d.h. die Richtung des Erdumlaufs um unser Zentralgestirn fällt mit der Richtung der Rotation der Sonne zusammen.
Die Rotationsdauer ist allerdings im Äquatorbereich eine andere als in polnahen Gebieten. Diese Erscheinung wird als differenzielle Rotation bezeichnet. Am Äquator beträgt die siderische Rotationsdauer etwa 25 Tage, bei einer Breite von 60° bereits 31 Tage und in den polnahen Bereichen 37 Tage.
Aus den Bahndaten lässt sich die Masse der Sonne berechnen.
Die Leuchtkraft der Sonne
Als Leuchtkraft eines Himmelskörpers wird die von ihm je Sekunde ins All abgestrahlte Energie bezeichnet. Im physikalischen Sinn ist also die Leuchtkraft eine Strahlungsleistung .
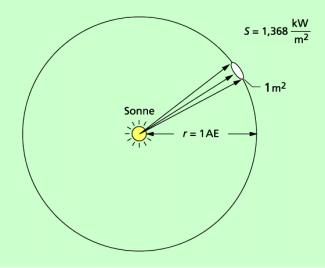
Die Sonnenleuchtkraft kann nicht direkt gemessen werden. Sie wird über die Solarkonstante ermittelt. Das ist die von der Sonne abgestrahlte Energie pro Zeiteinheit, die in Erdentfernung senkrecht auf einen Quadratmeter trifft. In Erdentfernung hat die Solarkonstante einen Wert von:
Summiert man über eine Kugelfläche auf (Bild 4), so erhält man aus dieser Angabe für die Leuchtkraft der Sonne:
Die Oberflächentemperatur der Sonne
Die Oberflächentemperatur erhält man aus Strahlungsmessung en unseres Zentralgestirns. Eine genaue Temperaturbestimmung eines strahlenden Körpers ist nur durchführbar, wenn der physikalische Zustand des Strahlers und die Gesetze zwischen seinem Zustand, der Temperatur und der emittierten Strahlung bekannt sind. Diese Kenntnisse besitzen wir von der Sonnenoberfläche nahezu vollständig. Man wendet das Modell des schwarzen Strahlers auf die Sonne an.
Nach dem Strahlungsgesetz von STEFAN und BOLTZMANN ergibt sich für die Sonne:
Die so berechnete Temperatur wird als effektive Temperatur bezeichnet. Setzt man die entsprechenden Werte ein, so ergibt sich eine effektive Oberflächentemperatur der Sonne von 5 770 K. Man beachte: Dieser Wert ist ein ungefährer Wert, da hinter der Berechnung die Modellierung schwarzer Strahler steht.
Geht man z. B. vom Strahlungsmaximum der Sonne aus und berechnet man die Temperatur nach dem wienschen Verschiebungsgesetz, dann erhält man eine Oberflächentemperatur der Sonne von 6 100 K.
Die Leuchtkraft der Sonne kann man mithilfe der Solarkonstanten bestimmen.
differentielle Rotation Rotationsdauer Leuchtkraft Strahlungsleistung Zentralgestirn Solarkonstante Oberflächentemperatur Sonne effektive Temperatur Strahlungsmessungen Masse der Sonne wiensches Verschiebungsgesetz Strahlungsgesetz von STEFAN und BOLTZMANN mittlere Dichte der Sonne Zustandsgrößen Durchmesser Radius
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 