Masse und Energie – die Kernbindungsenergie

Bei jeder freiwillig ablaufenden Kernreaktion ist die Gesamtmasse der neu gebildeten Kerne kleiner als die Gesamtmasse der Ausgangskomponenten. Diese Massendifferenz $\Delta$m wird als Massendefekt bezeichnet. In einem 1905 erschienenen Beitrag von ALBERT EINSTEIN unter dem Titel „Ist die Trägheit eines Körpers von seinem Energiegehalt abhängig?“ stellte er fest:
„Die Masse eines Körpers ist ein Maß für dessen Energiegehalt“.

Den quantitativen Zusammenhang zwischen Masse und Energie gab er in Form einer Gleichung an, die sicher zu den berühmtesten und bekanntesten Gleichungen der Physik gehört. Sie lautet:

$\begin{array}{l}E=m\cdot c^2\\ E=\text{Gesamtenergie eines Körpers}\\ m=\text{Masse eines Körpers}\\ c=\text{Lichtgeschwindigkeit}\end{array}$

Mithilfe der EINSTEIN-Gleichung kann der Energiegewinn berechnet werden, der sich aus dem Massendefekt bei Kernreaktionen ergibt.
Demnach ist die Massenänderung eines Körpers seiner Energieänderung direkt proportional. Da die Lichtgeschwindigkeit c sehr groß ist, bewirkt eine kleine Massenänderung bereits eine verhältnismäßig große Änderung der Energie eines Körpers.

Dieser Zusammenhang ist die Grundlage der Energiegewinnung bei der Kernfusion.
Die molare Masse eines He-Kerns beträgt 4,00150 g/mol. Die Summe der Einzelmassen von je zwei Protonen (je Proton = 1,00728 g/mol) und Neutronen (je Neutron = 1,00867 g/mol) ergibt 4,03190 g/mol. Die Differenz zwischen der Summe der Einzelmassen zweier Neutronen und Protonen sowie der Masse des He-Kerns beträgt also 0,03040 g/mol. Rechnet man diese vermeintlich geringe Massendifferenz nach der Einstein-Gleichung in Energie um, so stellt man fest, dass dieser Massendifferenz ein enormes Energieäquivalent entspricht.

$\begin{array}{l}E\text{=}m·c^2\\ \text{= 0}\text{,0304}·{\text{10}}^{\text{–3}}\text{kg/mol}·{\text{(3}}^{\text{,00}}\\ \text{=}\text{2}\text{,74}·{\text{10}}^{\text{12}}\text{kg}·{\text{m}}^2{\text{/s}}^2·\text{mol}\\ \text{=}\mathrm{2,74}·{10}^9\text{kJ/mol}\end{array}$

Die Massenänderung $\Delta \text{m}$ bei chemischen Reaktionen ist so klein, dass man sie nicht messen kann. Deshalb ist auch das „Gesetz von der Erhaltung der Masse“ im Prinzip richtig.
Da bei Kernreaktionen jedoch wesentlich höhere Energiebeträge umgesetzt werden, sind Masseänderungen hierbei nicht mehr vernachlässigbar.

Beispiel: Kernspaltung

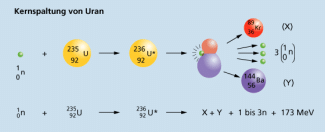
Kernspaltung bedeutet, dass Atomkerne von Elementen spontan oder durch äußere Beeinflussung in Kerne leichterer Elemente zerfallen und dabei Energie freigesetzt wird. Nach der Äquivalenz von Energie und Masse entspricht einer Energiefreisetzung eine Verringerung der Masse. So erfolgt beispielsweise die Spaltung von Uran-235 entsprechend der Gleichung:

${}_{92}{}^{235}\text{U}+{}_0{}^1\text{n}\to {}_{56}{}^{143}\text{B}\text{a}+{}_{36}{}^{90}\text{K}\text{r}+3\cdot \left({}_0{}^1\text{n}\right)+\Delta E$

Aus dieser Reaktionsgleichung folgt die Massebilanz bei der Kernspaltung:

$\begin{array}{l}\text{vor der Spaltung:}\\ {}_{\text{92}}{}^{\text{235}}\text{U}\text{: 235}\text{,0439}u\\ {}_{\text{0}}{}^{\text{1}}\text{n}\text{: 1}\text{,00898}u\\ \text{\_\_\_\_\_\_\_\_\_\_\_}\\ \text{236}\text{,0529}u\\ \\ \text{nach der Spaltung:}\\ {}_{\text{56}}{}^{143}\text{B}\text{a: 142}\text{,9084}u\\ {}_{\text{36}}{}^{\text{90}}\text{K}\text{r: 89}\text{,9043}u\\ 3\cdot \left({}_{\text{0}}{}^{\text{1}}\text{n}\right):\text{3}\text{,0296}u\\ \text{\_\_\_\_\_\_\_\_\_\_}\\ \text{235}\text{,8396}u\\ \Delta m=\mathrm{0,2133}u\\ \end{array}$

Diesem Massendefekt entspricht eine Energie, die bei der Kernspaltung freigesetzt wird:

$\begin{array}{l}E=\Delta m\cdot c^2\\ E=\mathrm{0,21833}\cdot \mathrm{1,661}\cdot {10}^{-27}\text{kg}\cdot {\left(\mathrm{2,99}792\cdot {10}^8\frac{\text{m}}{\text{s}}\right)}^2\\ E=\mathrm{3,18}\cdot {10}^{-11}\text{J}\\ E=198\text{MeV}\end{array}$

Das bedeutet: Bei der Kernspaltung ist die Masse vor der Spaltung größer als nach der Spaltung. Dem Massendefekt entspricht bei der Spaltung eines Urankerns eine Energie von ca. 200 MeV.

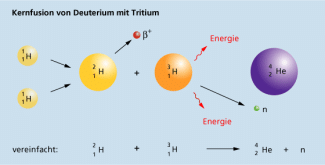
Beispiel: Kernfusion

Kernfusion im Inneren der Sonne ist die Quelle der Sonnenenergie, die Voraussetzung für die Entstehung und Entwicklung des Lebens auf der Erde ist. In jeder Sekunde verschmelzen im Inneren der Sonne 567 Mio. Tonnen Wasserstoff zu 562,8 Mio. Tonnen Helium (Bild 3). Der Massendefekt beträgt damit in jeder Sekunde 4,2 Mio. Tonnen. Daraus ergibt sich die Energie, die in jeder Sekunde von der Sonne abgegeben wird:

$\begin{array}{l}E=\Delta m\cdot c^2\\ E=\mathrm{4,2}\cdot {10}^9\text{kg}\cdot {\left(\mathrm{2,99792}\cdot {10}^8\frac{\text{m}}{\text{s}}\right)}^2\\ E=\mathrm{3,8}\cdot {10}^{26}\text{J}\end{array}$

Das entspricht einer Strahlungsleistung der Sonne (in der Astronomie als Leuchtkraft L bezeichnet) von: $L=\mathrm{3,8}\cdot {10}^{26}\text{W}$

Beispiel: Kernbindungsenergie

Als Kernbindungsenergie wird die Energie bezeichnet, die erforderlich wäre, um einen Kern in seine Bestandteile zu zerlegen. Es ist zugleich die Energie, die frei wird, wenn ein Kern aus seinen Bestandteilen zusammengefügt wird.
Dabei gilt: Die Masse der Bestandteile eines Kerns ist größer als die Kernmasse. Beim Zusammenfügen der Bestandteile tritt ein Massendefekt auf, der der Kernbindungsenergie äquivalent ist.
Damit kann man für einzelne Atomkerne die Kernbindungsenergie berechnen. Die Kernbindungsenergie hängt von der Nukleonenzahl ab. Die mittlere Bindungsenergie je Nukleon liegt zwischen 7 MeV und 9 MeV.

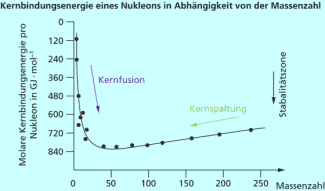
Es gibt zwei prinzipielle Möglichkeiten, die Kernbindungsenergie und damit die Stabilität von Atomkernen auszudrücken: entweder durch die molare Kernbindungsenergie bezogen auf den Atomkern oder die molare Kernbindungsenergie bezogen auf ein Nukleon.
Die Kernbindungsenergie von Atomkernen wächst mit steigender Atommasse, d. h. mit steigender Anzahl an Nukleonen. Einen besseren Eindruck von den energetischen Verhältnissen vermittelt jedoch die molare Kernbindungsenergie eines Nukleons. Man errechnet diese durch Division der molaren Kernbindungsenergie eines Isotops durch die Zahl seiner Nukleonen.
Sowohl die Spaltung großer Atomkerne wie auch die Fusion kleiner Atomkerne ist exotherm. Das bedeutet, dass Isotope, die schwerer sind als Eisen-56 sich durch Spaltung ihrer Atomkerne unter Bildung leichterer Kerne stabilisieren können, weil sie dabei Energie abgeben. Andererseits nimmt der Energiegewinn bei der Bildung von Kernen aus Protonen und Neutronen bis zur Bildung des Eisen-56-Kerns ständig zu und erreicht hier sein Maximum. Diese beiden Tendenzen sind die Grundlage für die Vorgänge der Kernspaltung oder Kernfusion.