Ableitung der Tangens- und der Kotangensfunktion
Im Folgenden wird gezeigt, dass die Tangensfunktion in ihrem gesamten Definitionsbereich differenzierbar ist und dort die Ableitungsfunktion besitzt.
Die Ableitung der Kotangensfunktion kann auf analogem Wege ermittelt werden.
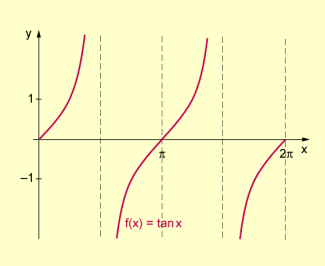
Dazu betrachten wir den Graph der Tangensfunktion im Intervall von 0 bis .
-
Graph der Tangensfunktion
Um die Ableitung der Tangensfunktion zu ermitteln, gehen wir von der Definitionsgleichung aus und wenden die Quotientenregel der Differenzialrechnung an.
Es gilt dann:
Für die Ableitung der Tangensfunktion gilt also:
- Die Tangensfunktion ist in ihrem gesamten Definitionsbereich differenzierbar und besitzt dort die Ableitungsfunktion
Beispiel: Es ist die 1. Ableitung der Funktion zu ermitteln.
Wir wenden die Produktregel der Differenzialrechnung an.
Mit gilt dann:
Die Ableitung der Kotangensfunktion kann auf analogem Wege ermittelt werden.
In diesem Fall wendet man die Quotientenregel auf die Definitionsgleichung der Kotangensfunktion oder an und erhält als Ableitung der Kotangensfunktion:
- Die Kotangensfunktion ist in ihrem gesamten Definitionsbereich differenzierbar und besitzt dort die Ableitungsfunktion
-
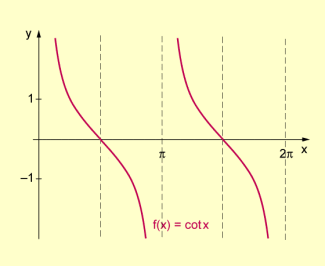
Graph der Kotangensfunktion