Anwendungen von Zahlenfolgen

Im Folgenden werden einige Aufgaben vorgestellt, die mithilfe des Wissens über (arithmetische und geometrische) Zahlenfolgen gelöst werden können.

Beispiel 1

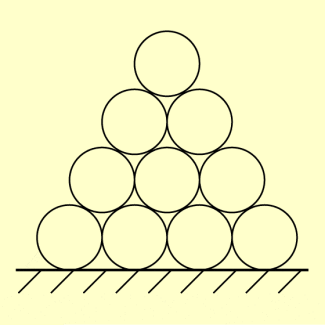
Auf einem Lagerplatz sind Rohre in der Weise gestapelt, wie die Abbildung zeigt.
a) Wie viele Rohre können gestapelt werden, wenn in der ersten Reihe zwölf Rohre liegen?
b) Wie viele Rohre müssen (mindestens) in der ersten Reihe liegen, wenn 140 Rohre so gestapelt werden sollen?

Lösung der Teilaufgabe a):
In jeder Reihe liegt ein Rohr weniger als in der vorhergehenden. Damit ergibt sich die (endliche) Zahlenfolge $\left(a_n\right)=\left\{12;11;\mathrm{...};2;1\right\}$. Hierbei handelt es sich um eine arithmetische Folge mit $a_1=12;d=-1$ und $n=12$. Gesucht ist $s_{12}$.

Für die Summe $s_{12}$ gilt:
$\begin{array}{l}{s}_n=\frac{n}{2}\left(a_1+a_n\right)\\ s_{12}=6\cdot (12+1)=78\end{array}$

Es können 78 Rohre gestapelt werden.

Lösung der Teilaufgabe b):
Es gilt $s_n\ge 140;d=-1$ und $a_1=n$. Dann folgt:
$s_n=\frac{n}{2}(n+1)=\frac{n^2+n}{2}\ge 140$

Das führt auf die quadratische (Un-)Gleichung $n^2+n-280\ge 0$ mit den formalen Lösungen $n_{1;2}\ge -\mathrm{0,5}\pm \sqrt{\mathrm{180,25}}$. Da n eine natürliche Zahl sein muss, erhalten wir als (einzige) Lösung $n=17$.

Anmerkung: Für die Summe $s_n$ der ersten n natürlichen Zahlen gilt $s_n=\frac{n^2+n}{2}$.

Beispiel 2

In einem Zirkuszelt befinden sich in der ersten Sitzreihe 80 Plätze, in jeder der darüber angeordneten Reihen jeweils sechs Plätze mehr. Insgesamt gebt es zehn Sitzreihen. Wie viel Plätze sind im Zelt?

Lösung: Es handelt sich um eine arithmetische Folge mit $a_1=80;d=6$ und $n=10$, und es gilt:
$\begin{array}{l}{s}_n=\frac{n}{2}\left[2a_1+(n-1)\cdot d\right]\\ s_{10}=5(2\cdot 80+9\cdot 6)=5\cdot 214=1070\end{array}$

Im Zelt gibt es 1070 Plätze.

Beispiel 3

Die Halbwertszeit des radioaktiven Iod-Isotops
I-131 beträgt 8,0 Tage.
(Die Halbwertszeit gibt die Zeitspanne an, in der jeweils die Hälfte der vorhandenen Masse zerfällt.)
a) Wie viel ist von 10 Gramm I-131 nach 80 Tagen noch übrig?
b) Nach welcher Zeit sind von 10 Gramm I-131 noch 5 mg vorhanden?

Lösung der Teilaufgabe a):
Der Anfangswert und die jeweils nach Abschnitten von 8,0 Tagen noch vorhandene Masse ergeben nachstehende Zahlenfolge:
$10g;5g;\mathrm{2,5}g;\mathrm{1,25}g;\mathrm{...}$

Es liegt eine geometrische Folge mit $a_1=10$ und $q=\mathrm{0,5}$ (Angabe der Folgeglieder hier und im Folgenden ohne Maßeinheit) vor.

Die nach $80(=10\cdot \mathrm{8,0})$ Tagen noch vorhandene Masse ist dann das Glied $a_{11}$ der genannten geometrischen Folge, und es gilt:
$\begin{array}{l}{a}_{11}=a_1\cdot q^{10}\\ =10\cdot {(\mathrm{0,5})}^{10}=\mathrm{0,009}765625\end{array}$

Nach 80 Tagen sind also noch etwa 9,8 mg des Iod-Isotops vorhanden.

Lösung der Teilaufgabe b):
Von der obigen geometrischen Folge sind $a_1=10$ und $a_n=\mathrm{0,005}$ gegeben, n ist gesucht. Es gilt:
$q^{n-1}=\frac{a_n}{a_1}$

Logarithmieren (zur beliebigen Basis, hier zur Basis 10) ergibt dann
$\begin{array}{l}\lg q^{n-1}=\lg \frac{a_n}{a_1}\\ (n-1)\cdot \lg q=lg\frac{a_n}{a_1}\Rightarrow n-1=\frac{lg\frac{a_n}{a_1}}{\lg q},\end{array}$
also
$n-1=\frac{\lg \mathrm{0,0005}}{\lg \mathrm{0,5}}\approx \mathrm{10,97}($ bzw. $n\approx \mathrm{11,97})$.

Nach knapp 88 Tagen sind noch 5 mg I-131 vorhanden.

Anmerkung: Hier zeigt sich die Grenze des mathematischen Modells Zahlenfolgen mit ihrem diskreten Definitionsbereich. Genauer kann der Sachverhalt mithilfe von Exponentialfunktionen beschrieben werden.

Beispiel 4

Für den Bau eines Brunnens wird eine Bohrung durchgeführt. Dabei kostet der erste Meter 15 Euro und jeder weitere 5 % mehr als der vorhergehende.
Wie hoch werden die Kosten für eine Bohrtiefe von 40 m?

Lösung: Es gilt $a_n=a_{n-1}\cdot \mathrm{1,05}$.
Damit liegt eine geometrische Folge mit $a_1=15$ und $q=\mathrm{1,05}$ vor.

Die Kosten für den vierzigsten Meter errechnen sich wie folgt:
$\begin{array}{l}{a}_{40}=a_1\cdot q^{39}\\ =15\cdot {\mathrm{1,05}}^{39}\approx \mathrm{100,57}\end{array}$

Interessanter ist natürlich die Frage nach den Gesamtkosten. Diese errechnen sich nach der Formel für die Partialsumme einer geometrischen Folge:
$s_{40}=15\cdot \frac{{\mathrm{1,05}}^{40}-1}{\mathrm{1,05}-1}\approx 1812$

Die Gesamtkosten belaufen sich damit auf etwa 1812 Euro.

Beispiel 5

Ein Bogen Papier habe eine Stärke von 0,20 mm.
Er wird 15-mal jeweils in der Mitte gefaltet.
Wie dick wird das Ganze nach 15-maligem Falten, wenn man die Zwischenräume vernachlässigt?

Lösung: Da sich die Dicke jeweils verdoppelt, liegt eine geometrische Folge mit $a_1=\mathrm{0,2}$ und $q=2$ vor. Gesucht ist $a_{16}$.

Es gilt:
$\begin{array}{l}{a}_{16}=a_1\cdot q^{15}\\ =\mathrm{0,2}\cdot 2^{15}=6\mathrm{553,6}(mm)\end{array}$

Es würde sich (falls man die Faltungen bewältigt) eine Dicke von mehr als 6,5 m ergeben.

Beispiel 6

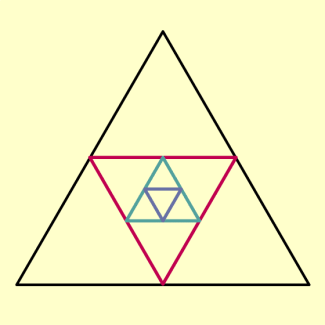
Einem gleichseitigen Dreieck wird ein wiederum gleichseitiges Dreieck einbeschrieben und zwar so, dass die Ecken des neuen auf den Seitenmitten des ursprünglichen Dreiecks liegen. Das Verfahren wird mehrfach wiederholt (siehe Abbildung).
Es ist der Flächeninhalt des fünften Dreiecks und die Summe der Flächeninhalte der ersten fünf Dreiecke zu berechnen, wenn das Ausgangsdreieck eine Seitenlänge von $a=10cm$ hat.

Lösung: Für den Flächeninhalt eines gleichseitigen Dreiecks gilt $A=\frac{a^2}{4}\sqrt{3}$. Die Fläche des jeweils einbeschriebenen Dreiecks beträgt ein Viertel der Fläche des vorhergehenden Dreiecks, es ist also:
$A_n=A_{n-1}\cdot \frac{1}{4}$

Damit liegt eine geometrische Folge mit $a_1=A_1=\frac{a^2}{4}\sqrt{3}$ und $q=\frac{1}{4}$ vor.
Gesucht sind $a_5=A_5$ und $s_5$.

Es gilt:
$\begin{array}{l}{A}_5=A_1\cdot {\left(\frac{1}{4}\right)}^4=\frac{a^2}{4^5}\sqrt{3}\\ =\frac{{(10cm)}^2}{4^5}\sqrt{3}\approx \mathrm{0,169}c{m}^2\end{array}$

Weiter ist:
$\begin{array}{l}{s}_5=A_1\cdot \frac{1-{(\mathrm{0,25})}^5}{1-\mathrm{0,25}}=\frac{a^2}{4}\sqrt{3}\cdot \frac{1-{(\mathrm{0,25})}^5}{\mathrm{0,75}}\\ =\frac{{(10cm)}^2}{4}\sqrt{3}\approx \mathrm{57,7}c{m}^2\end{array}$

Anmerkung: Die Folge der $s_n$ hat den Grenzwert $s=\frac{A_1}{1-q}=\frac{A_1}{\mathrm{0,75}}=\frac{4}{3}{A}_1=\frac{a^2}{3}\sqrt{3}$.

Beispiel 7

Man berechne die Summe der Umfänge aller Dreiecke, wenn das in Beispiel 6 beschriebene Verfahren unendlich oft fortgesetzt wird.

Lösung: Für die Dreiecksumfänge gilt $u_1=3a$ und $u_n=u_{n-1}\cdot \frac{1}{2}$. Damit liegt eine geometrische Folge mit $a_1=u_1$ und $q=\frac{1}{2}$ vor.
Die Partialsummenfolge hat den Grenzwert $s=\frac{u_1}{1-\mathrm{0,5}}=2u_1$. Die Summe der Umfänge aller Dreiecke ist also genauso groß wie der Umfang des Ausgangsdreiecks.

Andere typische Anwendungen geometrischer Zahlenfolgen sind Wachstumsprozesse und Zufallsprozesse.