Binomialkoeffizienten

Binomialkoeffizienten lassen sich nach der rekursiven Bildungsvorschrift des bekannten pascalschen Dreiecks ermitteln.

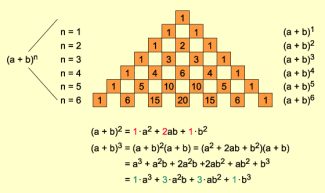
Ein solches Vorgehen hat aber den Nachteil, dass für die Berechnung der Koeffizienten von ${\left(a+b\right)}^n$ die von ${\left(a+b\right)}^{n-1}$ bekannt sein müssen.
Günstiger und effektiver ist es daher oftmals, die folgende Definition als explizite Bildungsvorschrift zu verwenden.

• Als Binomialkoeffizienten $\left(\begin{array}{c}n\\ k\end{array}\right)$(gelesen: n über k) bezeichnet man den Term $\left(\begin{array}{c}n\\ k\end{array}\right)=\frac{n!}{k!\cdot \left(n-k\right)!}=\frac{n\cdot \left(n-1\right)\cdot \mathrm{...}\cdot \left[n-\left(k-1\right)\right]}{1\cdot 2\cdot \mathrm{...}\cdot k}$
  mit $n,k\in \mathbb{N}$und $n\ge k$.

Anmerkung: Der in der Definition auftretende Term n! (gelesen: n Fakultät) besitzt die folgende explizite Bildungsvorschrift:
$n!=\{\begin{array}{cc}1\cdot 2\cdot \mathrm{...}\cdot n& fürn\in {\mathbb{N}}^{+}\\ 1& fürn=0\end{array}$

Die rekursive Bildungsvorschrift von n! lautet:
$\begin{array}{l}0!=1\\ \left(n+1\right)!=n!\cdot \left(n+1\right)fürn\in \mathbb{N}\end{array}$

• Beispiel: $\left(\begin{array}{c}10\\ 3\end{array}\right)=\frac{10!}{3!\cdot 7!}=\frac{8\cdot 9\cdot 10}{1\cdot 2\cdot 3}=120$

Die Binomialkoeffizienten sind bei vielen Taschenrechnern mittels einer speziellen (Tasten-)Funktion nCr auch direkt abrufbar.

Rechenregeln für Binomialkoeffizienten

• Regel 1: $\left(\begin{array}{c}n\\ 0\end{array}\right)=\left(\begin{array}{c}n\\ n\end{array}\right)=1$

Beweis:
$\begin{array}{l}\left(\begin{array}{c}n\\ 0\end{array}\right)=\frac{n!}{0!\cdot \left(n-0\right)!}=\frac{n!}{1\cdot n!}=1\\ \left(\begin{array}{c}n\\ n\end{array}\right)=\frac{n!}{n!\cdot \left(n-n\right)!}=\frac{n!}{n!\cdot 0!}=1w.z.b.w.\end{array}$
Im pascalschen Dreieck haben daher alle Randzahlen den Wert 1.

• Regel 2: $\left(\begin{array}{c}n\\ 1\end{array}\right)=\left(\begin{array}{c}n\\ n-1\end{array}\right)=n$

Im pascalschen Dreieck bilden daher sowohl die zweiten als auch die vorletzten Zeilenzahlen die Folge der natürlichen Zahlen.

• Regel 3: $\left(\begin{array}{c}n\\ k\end{array}\right)=\left(\begin{array}{c}n\\ n-k\end{array}\right)$

Daraus ergibt sich im pascalschen Dreieck die symmetrische Anordnung der Zahlen.

• Regel 4: $\left(\begin{array}{c}n\\ k\end{array}\right)+\left(\begin{array}{c}n\\ k+1\end{array}\right)=\left(\begin{array}{c}n+1\\ k+1\end{array}\right)$

Beweis:
Die linke Seite der zu beweisenden Gleichung wird schrittweise so umgeformt, bis man die rechte Seite erhält:
$\begin{array}{c}\left(\begin{array}{c}n\\ k\end{array}\right)+\left(\begin{array}{c}n\\ k+1\end{array}\right)=\frac{n!}{k!\cdot \left(n-k\right)!}+\frac{n!}{\left(k+1\right)!\cdot \left(n-k-1\right)!}\\ =\frac{n!\cdot \left(k+1\right)+n!\cdot \left(n-k\right)}{\left(k+1\right)!\cdot \left(n-k\right)!}=\frac{\cancel{n!\cdot k}+n!+n!\cdot n-\cancel{n!\cdot k}}{\left(k+1\right)!\cdot \left(n-k\right)!}\\ =\frac{n!\cdot \left(1+n\right)}{\left(k+1\right)!\cdot \left(n-k\right)!}=\frac{\left(n+1\right)!}{\left(k+1\right)!\cdot \left(n-k\right)!}\\ =\left(\begin{array}{c}n+1\\ k+1\end{array}\right)w.z.b.w.\end{array}$

Im pascalschen Dreieck entspricht diese Regel der folgenden rekursiven Bildungsvorschrift: Die inneren Zahlen jeder Zeile entstehen, indem die zwei darüber stehenden benachbarten Zahlen addiert werden.

• Regel 5: $\left(\begin{array}{c}n+1\\ k+1\end{array}\right)=\frac{n+1}{k+1}\cdot \left(\begin{array}{c}n\\ k\end{array}\right)$

Anmerkung: Die Regeln 2, 3 und 5 werden ähnlich wie die Regeln 1 und 4 mithilfe der allgemeinen Definition für Binomialkoeffizienten und der Kürzungsregel für Fakultäten bewiesen.

Im Folgenden werden einige Anwendungen der Binomialkoeffizienten angegeben.

1. Binomischer Lehrsatz:
   ${\left(a+b\right)}^n={\displaystyle \sum _{k=0}^n\left(\begin{array}{c}n\\ k\end{array}\right)}\cdot a^k{b}^{n-k}\left(n,k\in \mathbb{N}\right)$
   Spezialfall $\left(a=b=1\right)$ :
   $2^n={\displaystyle \sum _{k=0}^n\left(\begin{array}{c}n\\ k\end{array}\right)}$
    

2. Zählprinzip für Mengen
   Beim Zahlenlotto „6 aus 49“ gibt es insgesamt
   $\left(\begin{array}{c}49\\ 6\end{array}\right)=\frac{49!}{6!\cdot 43!}=\frac{44\cdot 45\cdot 46\cdot 47\cdot 48\cdot 49}{1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6}=13983816$
   verschiedene Tipps.
    
3. Urnenmodell ohne Zurücklegen
   Beim Zahlenlotto „6 aus 49“ beträgt die Wahrscheinlichkeit für genau k Richtige
   $\frac{\left(\begin{array}{c}6\\ k\end{array}\right)\cdot \left(\begin{array}{c}43\\ 6-k\end{array}\right)}{\left(\begin{array}{c}49\\ 6\end{array}\right)};\left(k=0;1;\mathrm{...};6\right).$
    
4. Binomialverteilung
   Die Wahrscheinlichkeit, beim viermaligen Werfen eines idealen Würfels, dessen Seitenflächen mit 1 bis 6 durchnummeriert sind, genau k Einsen zu werfen, beträgt:
   $\left(\begin{array}{c}4\\ k\end{array}\right)\cdot {\left(\frac{1}{6}\right)}^k\cdot {\left(\frac{5}{6}\right)}^{4-k}\left(k=0;1;2;3;4\right)$

Abschließend sollen noch zwei Verallgemeinerungen des Begriffes der Binomialkoeffizienten angegeben werden.

1. Verallgemeinerung:
   $\left(\begin{array}{c}\alpha \\ k\end{array}\right)=\frac{\alpha \cdot \left(\alpha -1\right)\cdot \mathrm{...}\cdot \left(\alpha -k-1\right)}{k!}\left(\alpha \in ℝ;k\in \mathbb{N}\right)$

Diese Verallgemeinerung wird in der Analysis angewandt (TAYLOR-Reihen von Funktionen) und kann auch häufig mit der Taschenrechner nCr-Funktion berechnet werden, z.B. ist:
$\begin{array}{l}\left(\begin{array}{c}\mathrm{1,7}\\ 3\end{array}\right)=\frac{\mathrm{1,7}\cdot \mathrm{0,7}\cdot \left(-\mathrm{0,3}\right)}{1\cdot 2\cdot 3}=-\mathrm{0,0595}\\ \left(\begin{array}{c}-3\\ 4\end{array}\right)=\frac{\left(-3\right)\cdot \left(-4\right)\cdot \left(-5\right)\cdot \left(-6\right)}{1\cdot 2\cdot 3\cdot 4}=15\\ \left(\begin{array}{c}3\\ 5\end{array}\right)=\frac{3\cdot 2\cdot 1\cdot 0\cdot \left(-1\right)}{1\cdot 2\cdot 3\cdot 4\cdot 5}=0\end{array}$

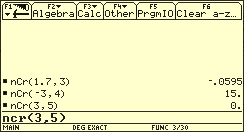
Die angegebene Verallgemeinerung des Begriffs der Binomialkoeffizienten wird bei der Angabe der mittels TAYLOR-Entwicklung gewonnenen binomischen Reihe genutzt. Es gilt:
${\left(1+x\right)}^{\alpha }=1+\left(\begin{array}{c}\alpha \\ 1\end{array}\right)x+\left(\begin{array}{c}\alpha \\ 2\end{array}\right)x^2+\mathrm{...}$

Dies ermöglicht z.B. die Angabe von Näherungsformeln wie die folgende:
$\begin{array}{c}{\left(1+x\right)}^{{}^{\frac{1}{2}}}=\left(\begin{array}{c}\frac{1}{2}\\ 1\end{array}\right)x+\left(\begin{array}{c}\frac{1}{2}\\ 2\end{array}\right)x^2+\left(\begin{array}{c}\frac{1}{2}\\ 3\end{array}\right)x^3+\mathrm{...}\\ =1+\frac{1}{2}x+\frac{\frac{1}{2}\cdot \left(\frac{1}{2}-1\right)}{1\cdot 2}{x}^2+\frac{\frac{1}{2}\cdot \left(\frac{1}{2}-1\right)\cdot \left(\frac{1}{2}-2\right)}{1\cdot 2\cdot 3}{x}^3+\mathrm{...}\\ =1+\frac{1}{2}x-\frac{1}{8}{x}^2+\frac{1}{16}{x}^3\mp \mathrm{...}\end{array}$

2. Verallgemeinerung: Polynomialkoeffizienten
   $\left(\begin{array}{c}n\\ k_1{k}_2\mathrm{...}{k}_r\end{array}\right)=\frac{n!}{k_1!\cdot k_2!\cdot \mathrm{...}\cdot k_r!}mitn={\displaystyle \sum _{i=1}^r{k}_i}$