Die Laplace-Regel

Ein Problem des DE MÉRÉ und die LAPLACE-Regel

Auf den CHEVALIER DE MÉRÉ geht das folgende Problem zurück:
Es werden drei nicht gezinkte Würfel gleichzeitig geworfen. Sowohl für das Auftreten der Augensumme 11 als auch für das der Augensumme 12 gibt es jeweils sechs Würfelkonstellationen, und zwar
$\left(1;4;6\right)\left(1;5;5\right)\left(2;3;6\right)\left(2;4;5\right)\left(3;3;5\right)\left(3;4;4\right)$
bzw.
$\left(1;5;6\right)\left(2;5;5\right)\left(2;4;6\right)\left(3;4;5\right)\left(3;3;6\right)\left(4;4;4\right).$

Daraus schlussfolgerte DE MÉRÉ, dass beide Augensummen mit der gleichen Chance auftreten müssten. Andererseits hatte er aber beobachtet, dass die Augensumme 11 häufiger auftrat als die Augensumme 12.

Die Wahrscheinlichkeiten derartiger zusammengesetzter Ereignisse können mit der von PIERRE SIMON LAPLACE (1749 bis 1827) formulierten Regel berechnet werden:

Die Wahrscheinlichkeit für die Existenz eines Ereignisses ist also nichts anderes als das Verhältnis der Anzahl der günstigen Fälle zu der aller möglichen Fälle, wenn wir außerdem keinen Grund sehen, weswegen einer dieser Fälle leichter einträte als ein anderer. Sie kann folglich dargestellt werden durch einen Bruch, dessen Zähler die Anzahl der günstigen Fälle ist und dessen Nenner die aller möglichen Fälle.

• LAPLACE-Regel: Wenn die Wahrscheinlichkeitsverteilung einer endlichen Ergebnismenge $\Omega =\left\{e_1;e_2;\mathrm{...};e_n\right\}$eine Gleichverteilung mit $P\left(\left\{e_1\right\}\right)=P\left(\left\{e_2\right\}\right)=\mathrm{...}=P\left(\left\{e_n\right\}\right)=\frac{1}{n}$ ist, dann gilt für jedes Ereignis $A\subseteq \Omega$:
  $P\left(A\right)=\frac{\left|A\right|}{\left|\Omega \right|}=\frac{\text{Anzahl}\text{der}\text{für}\text{A}\text{günstigen}\text{Ergebnisse}}{\text{Anzahl}\text{aller}\text{möglichen}\text{Ergebnisse}}$

Hieraus können folgende Schlussfolgerungen gezogen werden:

1. Für atomare Ereignisse gilt $\left|A\right|=1$ und demzufolge entspricht die LAPLACE-Regel in diesem Fall der LAPLACE-Annahme.
2. Die Berechnung von Wahrscheinlichkeiten mit der LAPLACE-Regel ergibt stets eine rationale Zahl.
3. Mit der LAPLACE-Regel können Wahrscheinlichkeiten vor der Durchführung der Zufallsexperimente berechnet werden. In diesem Sinne handelt es sich um einen sogenannten A-priori-Ansatz (a priori, lat. – von vornherein).

Lösung des Paradoxons von DE MÉRÉ mithilfe der LAPLACE-Regel

Betrachtet werden darf nicht nur die Gesamtaugensumme, sondern es muss auch die Aufteilung der einzelnen Augen einer bestimmten Konstellation auf die drei Würfel berücksichtigt werden, um die Gleichwahrscheinlichkeit der atomaren Ereignisse zu gewährleisten.

Man bezeichnet deshalb die drei Würfel mit $W_1,W_2,W_3$ und deren Ergebnisse mit $w_1,w_2,w_3$. Dann gilt:
$\begin{array}{l}\Omega =\left\{\left(w_1;w_2;w_3\right)\text{:}{w}_1,w_2,w_3\in \left\{1;2;\mathrm{...};6\right\}\right\}\\ \Rightarrow \left|\Omega \right|=6^3=216\end{array}$

Für das Ereignis Augensumme 11 gibt es dann die folgenden 27 (günstigen) Würfelkonstellationen:
$\begin{array}{l}\left(1;4;6\right)\left(1;5;5\right)\left(1;6;4\right)\\ \left(2;3;6\right)\left(2;4;5\right)\left(2;5;4\right)\left(2;6;3\right)\\ \left(3;2;6\right)\left(3;3;5\right)\left(3;4;4\right)\left(3;5;3\right)\left(3;6;2\right)\\ \left(4;1;6\right)\left(4;2;5\right)\left(4;3;4\right)\left(4;4;3\right)\left(4;5;2\right)\left(4;6;1\right)\\ \left(5;1;5\right)\left(5;2;4\right)\left(5;3;3\right)\left(5;4;2\right)\left(5;5;1\right)\\ \left(6;1;4\right)\left(6;2;3\right)\left(6;3;2\right)\left(6;4;1\right)\end{array}$

Analog erhält man für das Ereignis Augensumme 12 die folgenden 25 (günstigen) geordneten Tripel:
$\begin{array}{l}\left(1;5;6\right)\left(1;6;5\right)\\ \left(2;4;6\right)\left(2;5;5\right)\left(2;6;4\right)\\ \left(3;3;6\right)\left(3;4;5\right)\left(3;5;4\right)\left(3;6;3\right)\\ \left(4;2;6\right)\left(4;3;5\right)\left(4;4;4\right)\left(4;5;3\right)\left(4;6;2\right)\\ \left(5;1;6\right)\left(5;2;5\right)\left(5;3;4\right)\left(5;4;3\right)\left(5;5;2\right)\left(5;6;1\right)\\ \left(6;1;5\right)\left(6;2;4\right)\left(6;3;3\right)\left(6;4;2\right)\left(6;5;1\right)\end{array}$

Somit erhält man:
$\begin{array}{l}P\left(\left\{Augensumme11\right\}\right)=\frac{27}{216}=\mathrm{0,125}\\ P\left(\left\{Augensumme12\right\}\right)=\frac{25}{216}\approx \mathrm{0,116}\end{array}$

Das rechnerische Ergebnis bestätigt also die praktischen Beobachtungen von DE MÉRÉ. Die folgende Abbildung zeigt die Ergebnisse von drei Simulationen mithilfe des Programms siangs3w.

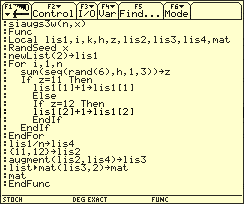
Sie stimmen mit den theoretisch gewonnenen Resulaten relativ gut überein. Die Beobachtungen von DE MÉRÉ beim Werfen von drei Würfeln kann man auch interaktiv überprüfen.

Der Fehler in DE MÉRÉS theoretischen Überlegungen bestand darin, dass die von ihm jeweils betrachteten sechs Möglichkeiten nicht gleichwahrscheinlich sind.

Anmerkung: Die Lösung der Aufgabe von DE MÉRÉ zeigt, dass das Bestimmen der Anzahl der für das betreffende Ereignis günstigen Ergebnisse und der Anzahl aller möglichen Ergebnisse bei komplizierten Ergebnismengen sehr aufwendig sein kann. Es erweist sich deshalb oftmals als sinnvoll, die entsprechenden Anzahlen mithilfe der Kombinatorik zu berechnen.

Den mit der LAPLACE-Regel ermittelten Wert
$P\left(A\right)=\frac{\left|A\right|}{\left|\Omega \right|}$
nennt man verschiedentlich klassische Wahrscheinlichkeit von A. Eine solche Bezeichnung hat insoweit ihre Berechtigung, da LAPLACE als Erster versuchte, den Begriff Wahrscheinlichkeit streng mathematisch zu fassen. Es darf dabei aber nicht außer Acht gelassen werden, dass mit einem solchem Ansatz wesentliche zufällige Vorgänge nicht erfasst werden können. Das betrifft vor allem jene, die nicht auf das Modell der Gleichverteilung zurückgeführt werden können, wie etwa das Werfen eines Kronverschlusses.