Geradenbüschel in der Ebene
- Definition: Die Menge der Geraden der Ebene, die durch einen festen Punkt geht, heißt Geradenbüschel.
-
Geradenbüschel in der Ebene
-
Schnittpunkt zweier Geraden eines Büschels
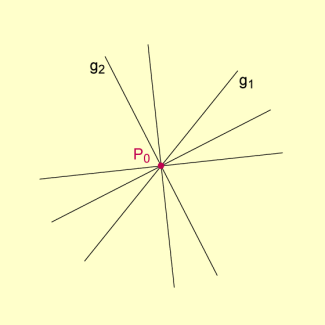
Da der Punkt schon als Schnittpunkt von zwei Geraden eines Büschels eindeutig bestimmt ist, kann man feststellen, dass jedes Geradenbüschel der Ebene durch zwei seiner Geraden eindeutig festgelegt ist.
Allgemeiner formuliert gilt sogar:
Zwei Geraden der Ebene, die nicht parallel zueinander sind, bestimmen eindeutig ein Geradenbüschel.
Um eine analytische Beschreibung eines Geradenbüschels zu gewinnen, werden zunächst zwei voneinander verschiedene Geraden betrachtet, die durch den Punkt gehen. Jede dieser beiden Geraden lässt sich z. B. durch den Ortsvektor zum Punkt und einen zugehörigen Normalenvektor beschreiben.
-
Normalenvektoren zweier Geraden eines Büschels
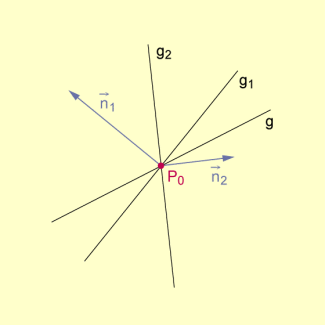
Aufgrund der Eigenschaft des Skalarprodukts zweier Vektoren gilt dann:
Jede andere Gerade g durch kann ebenfalls durch den Ortsvektor zu und einen Normalenvektor beschrieben werden. Es gilt dann:
Bedenkt man jetzt, dass nicht parallel zueinander sind, so sind auch die beiden Normalenvektoren nicht parallel zueinander bzw. sie sind linear unabhängig voneinander.
Folglich lässt sich der Vektor als Linearkombination von auffassen.
Es gilt , wobei p und q nicht gleichzeitig null sind.
Ersetzt man nun durch die Linearkombination aus in der Gleichung von g, so erhält man:
Damit lässt sich das durch bestimmte Geradenbüschel in der Ebene (und damit jede Gerade durch ) als eine Linearkombination der Gleichungen von zwei Geraden des Büschels auffassen.
- Satz: Sind zwei voneinander verschiedene Geraden durch , so beschreibt das zu gehörende Geradenbüschel.
Beschreibt man die beiden zueinander nicht parallelen Geraden durch ihre Gleichungen in allgemeiner Form
so beschreibt in analoger Weise![]()
das durch bestimmte Geradenbüschel.
Das heißt: Bei geeigneter Wahl der Parameter p und q lässt sich mit die Gleichung jeder Geraden durch denSchnittpunkt von beschreiben.
Bedenkt man nun, dass zur Bestimmung von die Gleichungen von als lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten aufgefasst werden können, dann bedeutet das Lösen dieses Systems jetzt: Man bestimme die Gleichungen der beiden Geraden des durch gebildeten Geradenbüschels, die zu den Koordinatenachsen parallel sind.
- Beispiel: Betrachtet werden die beiden Geraden mit den Gleichungen
: 3 x + 4y - 16 = 0 und
: x - 2y - 2 = 0.
-
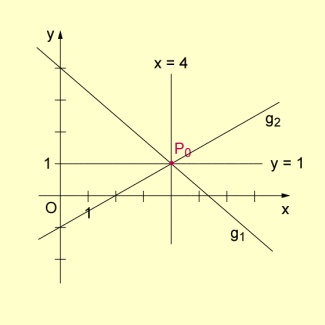
Spezielles Geradenbüschel in der Ebene
Die Gleichung p ·(3x + 4y - 16) + q · (x - 2y - 2) = 0 bzw.
(3p + q) x + (4p - 2q) y - (16p + 2q) = 0 (*)
beschreibt dann eine beliebige Gerade des Geradenbüschels, das durch aufgespannt wird.
Zur Bestimmung der Koordinaten des Schnittpunktes von werden die Gleichungen der Geraden des Büschels ermittelt, die parallel zu den Koordinatenachsen sind, also Gleichungen vom Typ x = a bzw. y = b besitzen.
Die Gerade des Büschels, die zur x-Achse parallel ist, erhält man, wenn der Koeffizient von x in (*) gleich 0 ist, also 3p + q = 0 gilt. Dies ist z. B. für p = 1 und q = -3 erfüllt. Mit diesen Werten wird (*) zu 10y -10 = 0, also y = 1.
Die Gerade des Büschels, die zur y-Achse parallel ist, erhält man analog, wenn der Koeffizient von y in (*) gleich null ist, also wenn 4p - 2q = 0 gilt. Das ist z. B. für p = 1 und q = 2 erfüllt. Mit diesen Werten wird (*) zu 5x - 20 = 0, also x = 4.
Damit ist aber der Schnittpunkt von .

