Kugelkoordinaten

Dieses Koordinatensystem stellt eine Erweiterung des Polarkoordinatensystems der Ebene dar und wird auch als räumliches Polarkoordinatensystem oder Kugelkoordinatensystem bezeichnet.

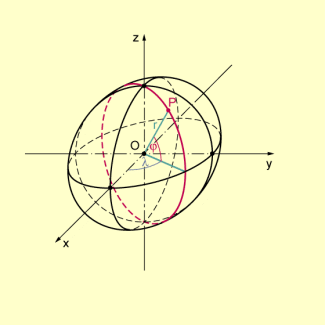
Die drei Koordinaten eines räumlichen Polarkoordinatensystems, sind die folgenden:

1. der Radius r als Abstand des Punktes P vom Ursprung O mit $r\ge 0$;
2. der Winkel $\lambda$ zwischen der positiven x-Achse und der Strecke $\overline{OP\text{'}}$, wobei $P\text{'}$ die Projektion von P in die xy-Ebene (Äquatorebene) darstellt vergleichbar mit den Längengraden der Erdkugel (mit $0\le \lambda <2\pi$);
3. der Winkel $\varphi$, der zwischen der xy-Ebene (Äquatorebene) und der Strecke $\overline{OP}$ gebildet wird (Breitengrade), wobei $\varphi$ Werte von $-\frac{\pi }{2}bis+\frac{\pi }{2}$ annehmen kann.

Die folgende Tabelle gibt die Umrechnungsmöglichkeiten von kartesischen Koordinaten in Kugelkoordinaten (und umgekehrt) an:

• Beispiel: Es sind die Kugelkoordinaten des (in kartesischen Koordinaten gegebenen) Punktes $P\left(5;12;13\right)$ zu ermitteln.

Durch Anwenden obiger Umrechnungen erhält man:
$\begin{array}{c}r=\sqrt{25+144+169}\approx \mathrm{18,385}\\ \lambda =arc\tan \frac{12}{5}=arc\tan \mathrm{2,4}\approx {\mathrm{67,38}}^{\circ }\\ \varphi =arc\tan \frac{13}{\sqrt{25+144}}=arc\tan 1={45}^{\circ }\end{array}$