Kegelschnitte in Polarkoordinatendarstellung

Im Folgenden wird das Vorgehen für die Parabel mit Brennpunkt im Koordinatenursprung demonstriert.

Die Gleichung (in kartesischen Koordinaten) dieser Parabel lautet wegen
$S\left(-\frac{p}{2};0\right)$: $y^2=2p\left(x+\frac{p}{2}\right)$

Einsetzen von $(\ast )$ergibt:
${\left(r\cdot \sin \varphi \right)}^2=2p\left(r\cdot \cos \varphi +\frac{p}{2}\right)$

Nach Umformen erhält man hieraus als Polargleichung der Parabel:
$r=\frac{p}{1-\cos \varphi }\left(0°\le \varphi <360°\right)$

Auch hier gilt eine Verallgemeinerung für alle Kegelschnitte.

• Die entsprechende allgemeine Polargleichung der Kegelschnitte hat folgende Form:
  $r=\frac{p}{1-\epsilon \cdot \cos \varphi }\left(0°\le \varphi <360°\right)$
  
  Es ergibt sich
  1. ein Kreis für $\epsilon =0$;
  2. eine Ellipse für $0<\epsilon <1$;
  3. eine Parabel für $\epsilon =1$;
  4. eine Hyperbel für $\epsilon >1$.

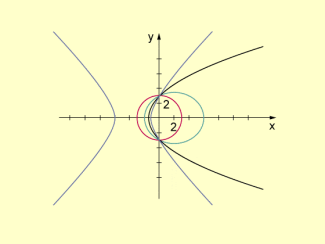
Beispiel: Für $p=3und\epsilon =0;\epsilon =\mathrm{0,5};\epsilon =1;\epsilon =\mathrm{1,5}$ entsteht zum Beispiel die in der folgenden Abbildung dargestellte Kurvenschar von Kegelschnitten.