Lineare Interpolation

Für viele Funktionen ist es nicht ganz einfach, Funktionswerte zu berechnen. Dies gilt insbesondere für transzendente Funktionen wie Winkel-, Logarithmus- und Exponentialfunktionen.

Natürlich kann man heutzutage viele derartige Funktionswerte durch einfachen Druck auf entsprechende Tasten des Taschenrechners erhalten. Die folgende Tabelle gibt einige Beispiele dafür an.

Dabei tauchen aber Fragen wie die folgenden auf:

1. Wie genau sind die vom Taschenrechner angegebenen Werte?
2. Wie hat man Funktionswerte früher ohne Rechenhilfsmittel (also vor der Erfindung des Taschenrechners) berechnet?

Die Genauigkeit eines Taschenrechners kann von Modell zu Modell unterschiedlich sein und ist in den Bedienungsanleitungen beschrieben. Sie ist im Allgemeinen aber recht hoch und somit für die meisten praktischen Probleme ausreichend. Beachten sollte man jedoch, dass die Genauigkeit oftmals nicht über den gesamten zur Verfügung stehenden Zahlenraum gleich, sondern an den Rändern meist geringer ist.

In der historischen Entwicklung waren Werte für Winkelfunktionen bereits in der Antike bekannt. Im Standardwerk zur Astronomie, dem Almagest von KLAUDIOS PTOLEMAIOS (um 85 bis um 165), sind für den Einheitskreis für Mittelpunktswinkel von $0°bis180°$ die zugehörigen Sehnenlängen tabelliert und zwar mit einer Schrittweite von 0,50. Der arabische Mathematiker AL-BÎRUNÎ (973 bis 1048) verfasste Sinustafeln , die auf acht Stellen genau waren. Auch Tangens- und Kotangenstafeln waren den arabischen Mathematikern bekannt.

Werte der Logarithmusfunktionen wurden in der ersten Hälfte des 17. Jahrhunderts tabelliert. Im Jahre 1614 gab JOHN NAPIER (1550 bis 1617) die erste Logarithmentafel heraus, 1620 erschienen die Tafeln von JOBST BÜRGI (1552 bis 1632) und 1617 die von HENRY BRIGGS (1561 bis 1631), der erstmals dekadische Logarithmen verwandte.
Die Berechnungen von Werten dieser und anderer transzendenten Funktionen waren aufwendig und wurden erst etwas einfacher, als man den Zusammenhang zu den Potenzreihen erkannte.

Dennoch bestand das Problem, zu Werten, die zwischen den tabellierten lagen, entsprechende Funktionswerte oder umgekehrt zu Funktionswerten, die nicht direkt in den Tabellen vorkamen, die entsprechenden Argumente zu ermitteln.
Wir betrachten dazu ein Beispiel (des Berechnens von Zwischenwerten).

• In einer Sinustafel findet man $\sin \mathrm{31,10}°=\mathrm{0,5165}$ und $\sin \mathrm{31,20}°=\mathrm{0,5180}$. Gesucht sind
  a) $\sin \mathrm{31,17}°$
  b) der Winkel $\alpha$ für $\sin \alpha =\mathrm{0,5173}$.

Lösung: Die Differenz der Argumente beträgt $D=\mathrm{0,10}°$, die der zugehörigen Funktionswerte beträgt $F=\mathrm{0,0015}$.

Teilaufgabe a): Gesucht ist die zur Differenz der Argumente $d=\mathrm{0,07}$ gehörende Differenz f der Funktionswerte. Man setzt die Proportion $f:F=d:D$ an und erhält:
$f=\frac{d\cdot F}{D}=\frac{\mathrm{0,07}\cdot \mathrm{0,0015}}{\mathrm{0,10}}=\mathrm{0,001}05$
Diesen Wert addiert man zu 0,5165, was zum Ergebnis $\sin \mathrm{31,17}°=\mathrm{0,517}55$ führt (ein Taschenrechner liefert 0,51578).

Teilaufgabe b): Gesucht ist die zur Differenz $f=\mathrm{0,008}$ der Funktionswerte gehörende Differenz d der Argumente. Man setzt die Proportion $d:D=f:F$ an und erhält:
$d=\frac{f\cdot D}{F}=\frac{\mathrm{0,008}\cdot \mathrm{0,1}}{\mathrm{0,0015}}=\mathrm{0,053}$
Diesen Wert addiert man zu 31,10, was zum Ergebnis $\alpha =\mathrm{31,153}°$ führt (ein Taschenrechner liefert $\mathrm{31,151}°$).

Das im Beispiel angewandte Verfahren heißt Interpolation (lat. interpolatio svw. Umgestaltung; lat. inter svw. zwischen).

Bei diesem Vorgehen sind von einer Funktion f(x) an den beiden Stellen $x_{1}und{x}_2$ die Funktionswerte $f\left(x_1\right)undf\left(x_2\right)$ gegeben. Für eine Stelle $x_z$, die zwischen $x_{1}und{x}_2$ liegt $\left(x_1<x_z<x_2\right)$ ist der Funktionswert $f\left(x_z\right)$ gesucht. Stetigkeit der Funktion f(x) wird vorausgesetzt.

Man ersetzt nun die Funktion zwischen den Punkten $P_{1}und{P}_2$ durch eine lineare Funktion, d.h., das Bild wird durch die Sekante zwischen $P_{1}und{P}_2$ ersetzt wie die folgende Abbildung zeigt.

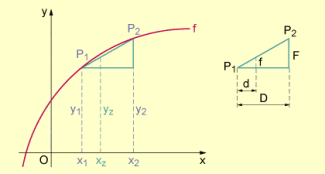
Setzt man $x_2-x_1=Dund{x}_z-x_1=d$ sowie $f\left(x_2\right)-f\left(x_1\right)=Fundf\left(x_z\right)-f\left(x_1\right)=f$,
so ergibt sich nach Strahlensatz die Proportion $F:f=D:d$.

Da man D und F kennt, kann man bei gegebenem d den Wert für f und daraus $f\left(x_z\right)$ oder bei gegebenem f den Wert für d und daraus den Wert für $x_z$ berechnen. Bei diesen Werten handelt es sich um Näherungswerte, deren Abweichung von den genauen Werten umso geringer ist, je weniger das Bild der Funktion f zwischen den Punkten $P_{1}und{P}_2$ von einer Geraden abweicht.

Da bei diesem Vorgehen das Bild der Funktion partiell durch eine Gerade ersetzt wird, nennt man das geschilderte Vorgehen auch lineare Interpolation.

Eine bessere Annäherung an das Bild einer Funktion f(x) und damit einer größere Genauigkeit des interpolierten Wertes erreicht man, wenn man mehr Punkte heranzieht und eine Funktion ermittelt, deren Bild durch alle diese Punkte geht. Dies leistet zum Beispiel das newtonsche Interpolationsverfahren.