Taylor-Entwicklung einiger trigonometrischer Funktionen

TAYLOR-Entwicklung der Funktion f(x) = sin x

Die Sinusfunktion soll an der Stelle $x_0=0$ nach TAYLOR entwickelt werden.

Für die Funktion f und ihre Ableitungen gilt:
$\begin{array}{l}f(x)=\sin xmitf(0)=0,\\ f^{\prime }(x)=\cos xmit{f}^{\prime }(0)=1,\\ f^{″}(x)=-\sin xmit{f}^{″}(0)=\mathrm{0,}\\ f^{‴}(x)=-\cos xmit{f}^{‴}(0)=-1,\\ f^{(4)}(x)=\sin xmit{f}^{(4)}(0)=0\end{array}$

und damit allgemein (wie man durch vollständige Induktion zeigen kann) für $k\in \mathbb{N}$
$\begin{array}{l}{f}^{(4k)}(x)=\sin xmit{f}^{(4k)}(0)=0,\\ f^{(4k+1)}(x)=\cos xmit{f}^{(4k+1)}(0)=1,\\ f^{(4k+2)}(x)=-\sin xmit{f}^{(4k+2)}(0)=\mathrm{0,}\\ f^{(4k+3)}(x)=-\cos xmit{f}^{(4k+3)}(0)=-1.\end{array}$

Im TAYLOR-Polynom der Sinusfunktion an der Stelle $x_0=0$ treten also nur Potenzen von x mit ungeraden Exponenten auf.

Mithilfe der allgemeinen taylorschen Formel erhalten wir
$f(x)=\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots +{(-1)}^{(k-1)}\cdot \frac{x^{2k-1}}{(2k-1)!}+{(-1)}^k\cdot \frac{x^{2k+1}}{(2k+1)!}\cdot \cos \vartheta x$ mit $0<\vartheta <1.$

Um beurteilen zu können, wie gut das in der obigen Gleichung aufgestellte TAYLOR-Polynom die Funktion f(x) = sin x an der Stelle $x_0=0$ approximiert, müssen wir das Restglied $R_{2k+1}(x)$ abschätzen:
$Wegen\left|\cos \vartheta x\right|\le 1ist{R}_{2k+1}(x)\le \frac{x^{2k+1}}{(2k+1)!}.$

Da $\underset{k\to \infty }{\lim }\frac{x^{2k+1}}{(2k+1)!}=\mathrm{0,}$ konvergiert auch das Restglied $R_{2k+1}(x)$ gegen null.

Erst jetzt können wir davon sprechen, dass sich die Sinusfunktion in der Umgebung von 0 durch das TAYLOR-Polynom approximieren lässt bzw. dass die Sinusfunktion in eine TAYLOR-Reihe entwickelt wurde:
$f(x)=\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots +{(-1)}^{(k-1)}\cdot \frac{x^{2k-1}}{(2k-1)!}+\dots$

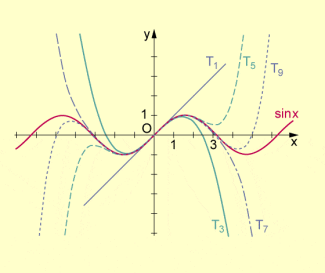
Die Abbildung zeigt die Sinusfunktion und die ersten fünf Schmiegparabeln.
(Man beachte, dass die Sinusfunktion eine ungerade Funktion ist.)

TAYLOR-Entwicklung der Funktion f(x) = cos x

Die Entwicklung der Kosinusfunktion erhält man auf analogem Wege:

Für die Ableitungen von f(x) = cos x gilt:
$\begin{array}{l}{f}^{(}{}^{2k)}(x)={(}^{-}\cdot \cos xund{f}^{(}{}^{2k)}(0)={(}^{-}bzw.\\ f^{(}{}^{2k+1)}(x)={(}^{-}\cdot \sin xund{f}^{(}{}^{2k+1)}(0)=\mathrm{0,}k=\mathrm{0,}\mathrm{1,}\mathrm{2,}\dots \end{array}$

Daraus folgt für die Entwicklung an der Stelle $x_0=0$
$\begin{array}{l}f(x)=\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots +{(}^{-}\cdot \frac{x^{2k}}{(2k)!}+R_{2k+2}\\ mit{R}_{2k+2}={(}^{-}\cdot \frac{x^{2k+2}}{(2k+2)!}\cdot \cos \delta x,0<\delta <1.\end{array}$

Bei festem x ist $\left|R_{2k+2}(x)\right|\le \frac{{\left|x\right|}^{2k+2}}{(2k+2)!}und\underset{k\to \infty }{\lim }\frac{{\left|x\right|}^{2k+2}}{(2k+2)!}=0.$

Auch die Kosinusfunktion lässt sich also in eine TAYLOR-Reihe entwickeln. Demzufolge kann man die Werte von cos x für beliebige x mit jeder geforderten Genauigkeit berechnen.

Derartige Approximationen nichtrationaler Funktionen sind eine wichtige Grundlage für entsprechende Rechenprozesse in Taschenrechnern und Computern.