Mehrstufige Zufallsexperimente

Betrachtet man reale Vorgänge mit einem zufälligen Ergebnis (etwa die Lebensdauer eines technischen Gerätes) genauer, so kann man vielfach feststellen, dass dieser zufällige Vorgang das Ergebnis einer Vielzahl von zufälligen Teilvorgängen ist, die neben- und nacheinander ablaufen und sich obendrein auch noch gegenseitig beeinflussen können.

Um einen solchen komplexen zufälligen Gesamtvorgang zu untersuchen, wird man bemüht sein, die spezifische innere Struktur seiner Teilvorgänge zu analysieren. Eine spezielle derartige Struktur ist ein mehrstufiges Zufallsexperiment.

• Definition: Besteht ein zufälliger Vorgang aus mehreren, nacheinander ablaufenden Teilvorgängen (oder aus Teilvorgängen, die als nacheinander ablaufend interpretiert werden können), so spricht man von einem mehrstufigen Zufallsexperiment, bei k Teilvorgängen $\left(mitk\in \mathbb{N}\backslash \left\{0\right\}\right)$ von einem k-stufigen Zufallsexperiment.

Um ein solches mehrstufiges Zufallsexperiment untersuchen zu können, muss man es zuerst mathematisch beschreiben – oder man kann auch sagen: mathematisch modellieren. Das erfordert insbesondere, die dazugehörige Ergebnismenge $\Omega$ und die Wahrscheinlichkeitsverteilung P anzugeben, wobei beide wesentlich vom konkreten Bedingungsgefüge und dem Beobachtungsziel des Zufallsexperiments abhängen.

Wir wollen dazu ein einfaches, überschaubares Beispiel in fünf Varianten betrachten.

• Beispiel: Axel und Bernd sind aktive Tischtennisspieler. Da sie schon oft gegeneinander gespielt haben, wissen sie aus Erfahrung, dass Axel unter „normalen Umständen“ einen Satz mit der Wahrscheinlichkeit $p=\mathrm{0,6}$ gewinnt und Bernd demzufolge mit der Wahrscheinlichkeit $1-p=\mathrm{0,4}$.
  (Beim Tischtennis wird ein Satz immer bis zur Entscheidung gespielt, ein Remis gibt es nicht.)

Anmerkung: A soll im Folgenden abkürzend verwendet werden, wenn Axel einen Satz gewinnt, und B, wenn dies bei Bernd der Fall ist.

Variante 1:
Aus Vergnügen spielen Axel und Bernd in ihrer Freizeit oftmals einfach fünf Sätze hintereinander. Nach jedem Satz registrieren sie, wer von beiden gewonnen hat. Da sie gut durchtrainiert sind, kann man davon ausgehen, dass jeder Satz im Prinzip unter gleichen Bedingungen und unabhängig vom Ergebnis des vorangegangenen ausgetragen wird. Gesucht ist die Wahrscheinlichkeitsverteilung für die Anzahl der Gewinnsätze von Axel.

Das Tischtennisspiel von Axel und Bernd kann als ein fünfstufiges Zufallsexperiment aufgefasst werden. Dessen Ergebnisse lassen sich durch 5-Tupel beschreiben, etwa $\left(A;B;B;A;A\right)$ oder $\left(B;B;B;A;A\right)$, d.h., es ist:
$\Omega =\left\{\left(e_1;e_2,\mathrm{...};e_5\right)mit{e}_i\in \left\{A;B\right\}undi=1;2;3;4;5\right\}$

Anmerkung: Generell können die Ergebnisse eines k-stufigen Zufallsexperiments durch k-Tupel beschrieben werden.

Da die einzelnen Sätze unter gleichen Bedingungen, unabhängig voneinander gespielt werden, kann dieses 5-stufige Zufallsexperiment durch eine BERNOULLI-Kette modelliert werden, sodass die Anzahl der Gewinnsätze von Axel binomialverteilt ist mit $n=5$ und $p=\mathrm{0,6}$.

Variante 2:
Für heute vereinbaren Axel und Bernd, wie im Wettkampf üblich, auf drei Gewinnsätze zu spielen, d.h., das Match hat derjenige gewonnen, der zuerst drei Sätze für sich entscheiden konnte.

Ein wichtiges Hilfsmittel zum Erfassen der Struktur eines mehrstufigen Zufallsexperiments ist das Baumdiagramm. Die folgende Abbildung zeigt das zugehörige Baumdiagramm für diese Spielvariante.

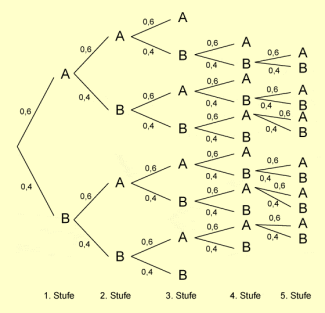
Es liegt also erneut ein 5-stufiges Zufallsexperiment vor.
Die Tupel, durch die die Ergebnisse des Zufallsexperiments beschrieben werden, haben allerdings eine unterschiedliche Länge, da es für einen Matchgewinn nicht immer erforderlich ist, fünf Sätze auszutragen.

Aus dem Baumdiagramm kann die Ergebnismenge $\Omega$ unmittelbar abgelesen werden:
$\Omega =\left\{\left(A;A;A\right),\left(A;A;B;A\right),\left(A;A;B;B;A\right),\mathrm{...,}\left(B;B;B\right)\right\}$

Die entsprechenden Wahrscheinlichkeiten lassen sich mithilfe der Pfadregeln ebenfalls dem Baumdiagramm entnehmen.

Variante 3:
Axel und Bernd treffen im Rahmen eines offiziellen Wettkampfes aufeinander. Axel kann unter diesen Bedingungen einen Satzverlust nervlich nicht so leicht verarbeiten, er wird dann zunehmend unsicherer. So beträgt seine Gewinnwahrscheinlichkeit gegenüber Bernd im Anschluss an genau einen für ihn verlorenen Satz nur noch 0,5 und im Anschluss an zwei hintereinander verlorenen Sätzen lediglich 0,4.

Diese Veränderung hat auf die Ergebnismenge $\Omega$ im Vergleich zur Variante 2 keine Auswirkungen, aber auf den Verlauf des Zufallsexperiments, denn auf jeder Stufe des Zufallsexperiments hängt der weitere Fortgang vom bisherigen Verlauf ab, also von bedingten Wahrscheinlichkeiten.

So hatten in der Variante 2 die Pfade $\left(A;A;B;B;A\right)$ und $\left(B;A;B;A;A\right)$ die gleiche Wahrscheinlichkeit ${\mathrm{0,6}}^3\cdot {\mathrm{0,4}}^2$. Jetzt gilt:
$\begin{array}{l}P\left(\left\{\left(A;A;B;B;A\right)\right\}\right)={\mathrm{0,6}}^2\cdot \mathrm{0,4}\cdot \mathrm{0,5}\cdot \mathrm{0,4}und\\ P\left(\left\{\left(B;A;B;A;A\right)\right\}\right)=\mathrm{0,4}\cdot \mathrm{0,5}\cdot \mathrm{0,4}\cdot \mathrm{0,5}\cdot \mathrm{0,6} \end{array}$

Variante 4:
Bernd hat gestern nach Variante 1 keinen Satz gewonnen. Er schlägt deshalb vor, heute so lange zu spielen, bis er einen Satz für sich entscheiden kann. Axel sagt:

„Damit wäre das Ende unseres heutigen Trainings also unbestimmt. Hoffentlich dauert es nicht so lange, denn ich muss noch etwas für die Schule machen.“

Theoretisch muss das so vereinbarte Tischtennisspiel kein Ende finden.
Die dazugehörige Ergebnismenge besteht aus abzählbar unendlich vielen Elementen und die einzelnen Tupel haben alle eine unterschiedliche „Länge“:
$\Omega =\left\{B,\left(A;B\right),\left(A;A;B\right),\left(A;A;A;B\right),\left(A;A;A;A;B\right),\mathrm{...}\right\}$

Nimmt man wie in Variante 1 an, dass die einzelnen Sätze unter gleichen Bedingungen und unabhängig voneinander ausgetragen werden (was mit zunehmender Spieldauer allerdings immer weniger realistisch ist), so ist die Anzahl der Sätze bis zum ersten Erfolg von Bernd geometrisch verteilt.

Variante 5:
Axel will Bernd etwas aufheitern, denn er schlägt vor, statt des zweiten und vierten Satzes (nach Variante 1) jeweils eine Partie Blitzschach zu spielen. Bernd gewinnt nämlich dabei mit einer Wahrscheinlichkeit von 0,6. Bei Axel beträgt diese lediglich 0,2. Die Wahrscheinlichkeit für ein Remis liegt bei ihnen erfahrungsgemäß bei 0,2.

Das Besondere an diesem fünfstufigen Zufallsexperiment besteht im Baumdiagramm darin, dass auf verschiedenen Stufen unterschiedliche Ergebnisse möglich sind: Die Ergebnisse und Wahrscheinlichkeiten der ersten, dritten und fünften Stufe unterscheiden sich von denen der zweiten und vierten Stufe.

Wenn ein Sieg von Axel beim Schach mit A', von Bernd mit B' und ein Remis mit R abgekürzt wird, so erhält man:
$\Omega =\left\{\left(e_1;e_2;\mathrm{...};e_5\right)mit{e}_1,e_3,e_5\in \left\{A;B\right\}und{e}_2,e_4\in \left\{A^{\prime };B^{\prime };R\right\}\right\}$