Definition der Binomialverteilung

• Definition: Eine Zufallsgröße X, welche die $0;1;2;\mathrm{...};n$ Werte mit den Wahrscheinlichkeiten
  $P\left(X=k\right)=B_{n;p}\left(\left\{k\right\}\right)=\left(\begin{array}{c}n\\ k\end{array}\right)\cdot p^k\cdot {\left(1-p\right)}^{n-k}$ für $k\in \left\{0;1;2;\mathrm{...};n\right\}$
  annimmt, heißt binomialverteilt mit den Parametern n und p oder auch kurz $B_{n;p}\text{-verteilt}$.
  Die zu X gehörende Wahrscheinlichkeitsverteilung nennt man Binomialverteilung mit den Parametern n und p.

Die Binomialverteilung genügt den drei kolmogorowschen Axiomen der Wahrscheinlichkeitstheorie.

Als abkürzende Schreibweise verwendet man $X\sim B_{n;p}$. Anstelle von $B_{n;p}\left(\left\{k\right\}\right)$ werden auch (in Anlehnung an die Wahrscheinlichkeitsfunktion als Stammfunktion ihrer Dichtefunktion bei stetigen Zufallsgrößen) die Bezeichnungen $f_B\left(k;n;p\right)$ oder die weniger genaue Schreibweise $b_{n;p}\left(k\right)$ verwendet.

Die Binomialverteilung ist die Wahrscheinlichkeitsverteilung des Urnenmodells „Ziehen mit Zurücklegen“: Einer Urne mit genau N Kugeln (M weißen, N – M roten) werden nacheinander genau n Kugeln „auf gut Glück“ und mit Zurücklegen entnommen.
Bezeichnet X die zufällige Anzahl der herausgegriffenen weißen Kugeln, so ist $X\sim B_{n;p}$ mit $p=\frac{M}{N}$.

Auf der Basis dieses Urnenmodells findet die Binomialverteilung breite Anwendung in der statistischen Qualitätskontrolle.

Eine Veranschaulichung der Binomialverteilung ist grafisch mithilfe eines Histogramms und experimentell mithilfe eines GALTON-Brettes möglich.

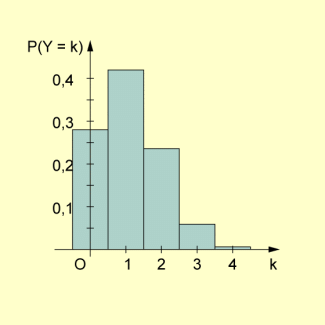
Binomialwahrscheinlichkeiten können mittels eines Taschenrechners (bzw. Computers) oder mit einem geeigneten Tafelwerk berechnet werden. In vielen Tafelwerken findet man $B_{n;p}\text{-Tabellen}$ für bestimmte Parameter n und p.

• Beispiel: Der laufenden Produktion von Speicherchips, die erfahrungsgemäß mit einer Wahrscheinlichkeit von 0,87 intakt sind, werden zehn Chips entnommen und dann kontrolliert. Mit welcher Wahrscheinlichkeit sind genau k intakte unter den zehn entnommenen Chips?

Unter der Annahme, dass die zehn Chips rein zufällig entnommen wurden, kann der obige Vorgang durch das folgende Urnenmodell beschrieben werden:
Einer Urne mit genau 100 Kugeln (87 weißen und 13 roten) werden nacheinander „auf gut Glück“ und mit Zurücklegen genau zehn Kugeln entnommen.
Bezeichnet X die zufällige Anzahl der intakten Chips unter den zehn entnommenen, so ist $X\sim B_{100;\mathrm{0,87}}$.

Die Aufgabe kann interaktiv mit der Funktion $\text{bi}\left(\mathrm{10,}\mathrm{0.87,}k\right)$ für $0\le k\le 10$ gelöst werden.

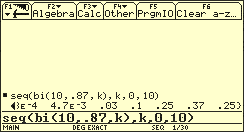
Für $k=9$ erhält man z.B.:
$P\left(X=9\right)=B_{10;\mathrm{0,87}}\left(\left\{9\right\}\right)=\left(\begin{array}{c}10\\ 9\end{array}\right)\cdot {\mathrm{0,87}}^9\cdot {\mathrm{0,13}}^1=bi\left(\mathrm{10,}\mathrm{.87,}9\right)\approx \mathrm{0,37}$

Anregung: Die Funktion $\text{bi}\left(n,p,k\right)$ gestattet es, die Wahrscheinlichkeit für beliebige Werte einer binomialverteilten Zufallsgröße zu berechnen. Auf diese Weise können auch die in der Aufgabenstellung des Beispiels vorgegebenen Werte interaktiv verändert werden.

Grafisch lassen sich die im Beispiel gewonnenen Ergebnisse mit einem Histogramm veranschaulichen. Dazu trägt man in einem Koordinatensystem auf dessen Abszissenachse die Werte $k=0;1;2;\mathrm{...};10$ und auf der Ordinatenachse die Wahrscheinlichkeiten $B_{10;\mathrm{0,87}}\left(\left\{k\right\}\right)$ ab.

Genutzt werden kann aber auch das Programm $\text{drawbi}\left(n,p\right)$ mit den Werten $n=10$ und $p=\mathrm{0,87}$.

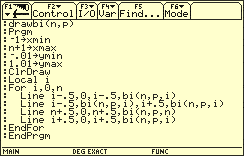
Interaktives Erkunden des Verlaufs der Binomialverteilung

Das Programm $\text{drawbi}\left(n,p\right)$ gestattet es, interaktiv weitere Einsichten zum Verlauf der Binomialverteilung zu gewinnen. Wenn man z.B. in $\text{drawbi}\left(n,p\right)$ für n einen bestimmten konstanten Wert eingibt und die Histogramme für verschiedene Werte von p miteinander vergleicht, kann man u.a. zu folgenden Ergebnissen gelangen:

1. Die Lage des höchsten Rechtecks wandert mit wachsenden p nach rechts. Das höchste Rechteck befindet sich bei $k=\mathrm{0,5}n$.
   Die Höhe des höchsten Rechtecks nimmt mit wachsenden p für $p\le \mathrm{0,5}$ ab und für $p\ge \mathrm{0,5}$ wieder zu. Das Histogramm „zerfließt“ am stärksten für $p=\mathrm{0,5}$.
2. Nur das Histogramm für $p=\mathrm{0,5}$ ist axialsymmetrisch, und zwar zur Geraden mit der Gleichung $k=\mathrm{0,5}n$. Je mehr p von 0,5 anweicht, desto asymmetrischer wird das Histogramm.
3. Das Histogramm von $B_{n;p}$ ist das Spiegelbild von $B_{n;1-p}$ bezüglich der Spiegelgeraden mit der Gleichung $k=\mathrm{0,5}n$.

Wenn man die von $\text{drawbi}\left(n,p\right)$ erzeugten Histogramme für konstantes p und variables n miteinander vergleicht, kann man u.a. zu folgenden Ergebnissen gelangen:

1. Die Histogramme werden mit wachsendem n zunehmend axialsymmetrischer.
2. Die Histogramme werden mit wachsendem n zunehmend breiter und zugleich flacher. Man kann davon sprechen, dass die Wahrscheinlichkeitsmasse 1 „zerfließt“.
3. Einige Histogramme (für die $\left(n+1\right)\cdot \mathrm{0,3}$ ganzzahlig ist) besitzen zwei nebeneinander liegende maximal hohe Rechtecke, und zwar für $k=\left(n+1\right)\cdot p-1$ und für $k=\left(n+1\right)\cdot p$

Die Berechnung und grafische Darstellung einer Binomialverteilung kann auch mithilfe einer Tabellenkalkulation erfolgen.