Zu den Anfängen der Integralrechnung
Während die Differenzialrechnung in der Untersuchung des Tangentenproblems wurzelt, war die Beschäftigung mit Inhaltsproblemen Ausgangspunkt für die Entstehung der Integralrechnung.
Dabei erregte das Inhaltsproblem sehr viel früher das Interesse als die Frage danach, ob für einen beliebigen Funktionsgraphen in einem vorgegebenen Punkt die Tangente an den Graphen existiert und wie man ihre Steigung ermitteln kann.
Bereits vor der Phase der griechisch-hellenistischen Mathematik waren einfache Methoden zur Berechnung der Flächeninhalte einzelner Vielecke und der Volumina einfacher Körper bekannt – gekleidet in die Form von „Rezepten“.
Einige dieser Handlungsanweisungen lieferten richtige und exakte Resultate, andere lediglich grobe Näherungen und einige auch falsche Ergebnisse.
So kann man den Quellen der ägyptischen Mathematik entnehmen, dass der Flächeninhalt von Dreiecken gleich dem halben Produkt einer Seite und der zugehörigen Höhe ist, aber der Flächeninhalt eines Kreises wurde als das Quadrat von seines Durchmessers angegeben.
Der Grundgedanke für die Ermittlung solcher Rezepte für die Flächeninhaltsberechnung bestand in der geschickten Zerlegung der jeweiligen Fläche und der anschließenden Neuanordnung ihrer Teile. Auf diese Weise erzielte die ägyptische Mathematik viele wichtige Resultate für die Berechnung von Vielecken.
Die erste exakte Quadratur einer Fläche, die nicht von Geraden begrenzt wird, gelang – soweit bekannt – um 450 v.Chr. HIPPOKRATES VON CHIOS. Er berechnete den Flächeninhalt mehrerer sogenannter „Kreismöndchen“.
Überhaupt geht der Begriff der Quadratur historisch gesehen auf das Problem zurück, eine Kreisfläche in ein flächeninhaltsgleiches Quadrat unter alleiniger Verwendung von Zirkel und Lineal zu verwandeln, während man heute „Quadratur“ allgemein für die Berechnung des Flächeninhalts ebener, nicht geradlinig begrenzter Flächenstücke verwendet.
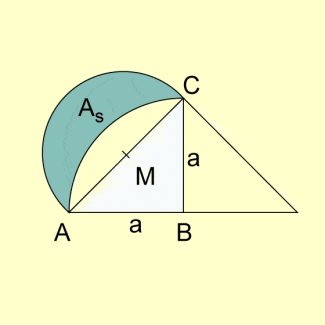
HIPPOKRATES gab so z.B. den Flächeninhalt der „Sichel“ in der folgenden Abbildung mit an. Diese „Sichel“ und das Dreieck ABC sind somit flächengleich.
-
Flächeninhalt einer „Sichel“
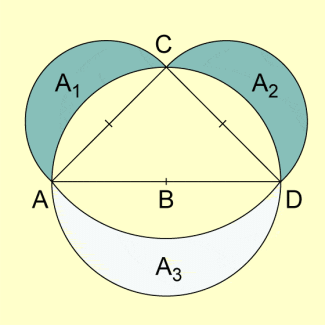
Durch analoge Überlegungen konnte HIPPOKRATES zeigen, dass für die Flächeninhalte der „Sicheln“ in der folgenden Abbildung gilt:
-
Möndchen des Hippokrates
In den folgenden 200 Jahren bemühten sich viele Mathematiker um die exakte Berechnung des Flächeninhaltes parabolisch, elliptisch und hyperbolisch begrenzter Flächen.
Um 260 v.Chr. gelang es dem griechischen Gelehrten ARCHIMEDES VON SYRAKUS (etwa 287 bis 212 v.Chr.), Parabelsegmente zu berechnen. Er entwickelte dazu die so genannte Exhaustionsmethode, d.h. er „schöpfte“ die unbekannte Fläche durch eine Folge berechenbarer Flächen aus.
Dann allerdings dauerte es fast 2000 Jahre, bis ARCHIMEDES auf diesem Gebiet Nachfolger in FRANCESCO BONAVENTURA CAVALIERI (1598 bis 1647), ISAAC NEWTON (1643 bis 1727) und GOTFRIED WILHELM LEIBNIZ (1646 bis 1716) fand. Diese entwickelten neben anderen Mathematikern Methoden, mit deren Hilfe Flächeninhaltsberechnungen für beliebige Flächen sehr leicht und schnell erfolgen können.
Die Exhaustionsmethode führte in Verbindung mit der Berechnung von Grenzwerten von Folgen (obere und untere Rechtecksummen) zum Begriff des bestimmten Integrals.

