Axiome, euklidische Geometrie
Im historischen Entstehungsprozess der Geometrie wurden relativ einfache, anschauliche Aussagen als Axiome gewählt, auf deren Grundlage sich die übrigen Sachverhalte beweisen ließen. Axiome sind also experimentellen Ursprungs, d. h. auch, dass sie gewisse einfache, anschauliche Eigenschaften des realen Raumes widerspiegeln. Die Axiome sind somit grundsätzliche Aussagen über die Grundbegriffe einer Geometrie, die dem betrachteten geometrischen System ohne Beweis hinzugefügt werden und auf deren Basis alle weiteren Aussagen des betrachteten Systems bewiesen werden.
Im historischen Entstehungsprozess der Geometrie wurden relativ einfache, anschauliche Aussagen als Axiome gewählt, auf deren Grundlage sich die übrigen Sachverhalte beweisen ließen. Axiome sind also experimentellen Ursprungs, d. h. auch, dass sie gewisse einfache, anschauliche Eigenschaften des realen Raumes widerspiegeln. Die Axiome sind somit grundsätzliche Aussagen über die Grundbegriffe einer Geometrie, die dem betrachteten geometrischen System ohne Beweis hinzugefügt werden und auf deren Basis alle weiteren Aussagen des betrachteten Systems bewiesen werden.
Axiome der Inzidenz (Verknüpfung)
I1 – Durch je zwei verschiedene Punkte geht eine und nur eine Gerade.
I2 – Auf jeder Geraden liegen mindestens zwei Punkte.
I3 – Es existieren drei Punkte, die nicht auf einer Geraden liegen.
-
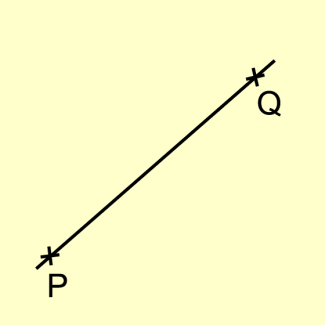
Durch zwei Punkte geht eine Gerade
Axiome der Anordnung
A1 – Von drei beliebigen paarweise verschiedenen Punkten einer Geraden liegt einer und nur einer zwischen den beiden anderen.
A2 – Zu zwei Punkten einer Geraden existiert auf dieser Geraden ein solcher dritter Punkt, dass der zweite zwischen dem ersten und dem dritten Punkt liegt.
A3 – Die Gerade g liege auf der Ebene ABC, wobei A, B und C nicht auf einer Geraden liegen, und gehe durch keinen der Punkte A, B und C.
Wenn g einen Punkt der Strecke AB enthält, so enthält sie auch einen Punkt der Strecke BC oder der Strecke AC.
Axiome der Kongruenz
K1 – Jede Strecke AB ist zu sich selbst und zur Strecke BA kongruent.
K2 – Sind A, B zwei verschiedene Punkte und ist R ein weiterer Punkt der Geraden g, so gibt es auf jeder von R ausgehenden Halbgeraden genau einen Punkt, C bzw. D, für den gilt:
K3 – Liegt ein Punkt A zwischen den Punkten B und C auf einer Geraden g und der Punkt A' zwischen den Punkten B' und C' auf einer anderen Geraden g', so gilt mit und auch .
K4 – Sind A, B, C drei nicht auf einer Geraden liegende Punkte und A', B' zwei andere Punkte, für die gilt , so gibt es auf jeder Seite der durch A' und B' bestimmten Geraden einen Punkt C' bzw. C'', sodass gilt:
bzw.
K5 – Sind A, B, C drei nicht auf einer Geraden liegende Punkte und ist D ein Punkt auf der durch A, B bestimmten Geraden, so folgt aus
und auch .
-
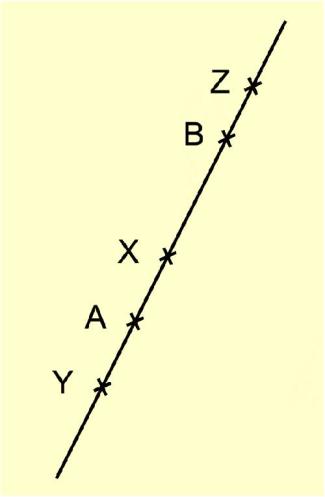
Lagebezeichnungen verschiedener Punkte auf einer Geraden
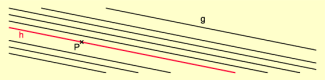
Axiom der Parallelen – Euklidisches Parallelenaxiom
EP – Zu einer Geraden gibt es durch einen nicht auf ihr liegenden Punkt höchstens eine Gerade, die die erste Gerade nicht schneidet.
Axiom der Stetigkeit – Archimedisches Axiom
S – Durch n-maliges Abtragen der Strecke auf einer Geraden erhalte man die Punkte und mit , wobei zwischen und liegt. Ist B ein Punkt der von nach gehenden Halbgerade, so gibt es eine natürliche Zahl m, sodass B zwischen und liegt.
Axiome der Bewegung
B1 – Jede Bewegung ist eine eineindeutige Abbildung des Raumes auf sich.
B2 – Liegen die Punkte A, B und C auf einer Geraden und liegt C zwischen A und B, so liegen auch die Bildpunkt A', B' und C' auf einer Geraden und es liegt C' zwischen A' und B'.
B3 – Die Nacheinanderausführung von Bewegungen ist wieder eine Bewegung.
B4 – Zu zwei Figuren gibt es höchstens eine und nur eine Bewegung, die die erste Figur auf die zweite Figur abbildet.
-
Euklidisches Parallelenaxiom