Bernoulli-Ketten

Wird ein Bernoulli-Versuch unabhängig voneinander n-mal (hintereinander) durchgeführt, so spricht man von einer Bernoulli-Kette der Länge n.
Viele in der Realität ablaufenden Vorgänge können als Bernoulli-Ketten aufgefasst werden. Das wohl klassischste Beispiel ist der n-fache Münzwurf mit dem Ergebnis Wappen als Erfolg und dem Ergebnis Zahl als Misserfolg (bzw. umgekehrt).

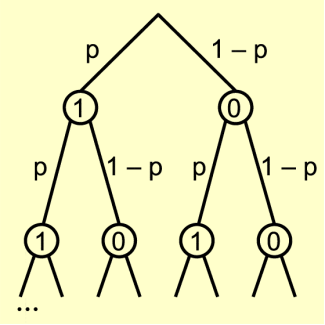
Wir betrachten einen Bernoulli-Versuch mit der Erfolgswahrscheinlichkeit p und bezeichnen den Erfolg mit „1“ und den Misserfolg mit „0“. Somit ist:

$P\left(1\right)=pundP\left(0\right)=1-p$

Wir führen den Bernoulli-Versuch n-mal durch. Das Ergebnis lässt sich dann als n-Tupel der Form $\left(e_1;e_2\mathrm{...}{e}_n\right)$darstellen, wobei die $e_i$ Nullen oder Einsen sind.
In der folgenden Tabelle sind einige Ergebnisse für den Fall n = 5 angegeben:

Allgemein gilt für die Wahrscheinlichkeit der Ergebnisse einer Bernoulli-Kette der Länge n und der Erfolgswahrscheinlichkeit p:

$P\left(\left(e_1;e_2\mathrm{...}{e}_n\right)\right)=p^{\text{Anzahl der Erfolge}}\cdot {\left(1-p\right)}^{\text{Anzahl der Misserfolge}}$
bzw.

$P\left(\left(e_1;e_2\mathrm{...}{e}_n\right)\right)=p^{\text{Anzahl der Erfolge}}\cdot {\left(1-p\right)}^{n-\text{Anzahl der Erfolge}}$

Hieraus folgt, dass jede Kette mit der gleichen Anzahl k an Erfolgen die gleiche Wahrscheinlichkeit hat.

Mithilfe der Kombinatorik können wir ermitteln, auf wie viele verschiedene Weisen eine Bernoulli-Kette der Länge n jeweils genau k Erfolge auftreten können. Das ist gleichbedeutend mit dem Problem, aus n Elementen k Elemente auszuwählen, und es gibt dafür insgesamt $\left(\begin{array}{c}n\\ k\end{array}\right)$ Möglichkeiten. In unserem obigen Beispiel für n = 5 gäbe es somit $\left(\begin{array}{c}5\\ 3\end{array}\right)=10$ Möglichkeiten für drei Erfolge.

Eine allgemeine Aussage über die Wahrscheinlichkeit des Auftretens von genau k Erfolgen bei einer Bernoulli-Kette der Länge n und der Erfolgswahrscheinlichkeit p macht die folgende sogenannte bernoullische Formel

$P\left(\text{genau k Erfolge}\right)=\left(\begin{array}{c}n\\ k\end{array}\right)\cdot p^k\cdot {\left(1-p\right)}^{n-k}(k=0;1\mathrm{...}n)$

Die Werte des als Binomialkoeffizient bezeichneten Ausdrucks $\left(\begin{array}{c}n\\ k\end{array}\right)$können dem pascalschen Zahlendreieck oder Tabellen entnommen (bzw. gemäß ihrer Definition berechnet) werden.
Die Anzahl der Erfolge in einer Bernoulli-Kette der Länge n wird durch die Zufallsgröße $S_n$ mit $S_n\left(e_1;e_2\mathrm{...}{e}_n\right)=e_1+e_2+\mathrm{...}+e_n$ beschrieben. Die dazugehörige Wahrscheinlichkeitsverteilung heißt Binomialverteilung.

Es wird fünf Mal mit einem idealen Würfel gewürfelt. Das Erzielen einer Sechs gelte als Erfolge, alles andere als Misserfolg.

Die folgende Tabelle gibt die Wahrscheinlichkeit für k Erfolge an.

Relativ einfach lässt sich die Wahrscheinlichkeit für mindestens einen Erfolg angeben. In diesem Fall gilt:

$P\left(\text{mindestens ein Erfolg}\right)=1-{\left(1-p\right)}^n$

Die Wahrscheinlichkeit, beim fünfmaligen Würfeln mindestens eine Sechs zu haben, ist somit $1-{\left(\frac{5}{6}\right)}^5\approx \mathrm{59,8}\%$, würfelt man zehnmal erhöht sie sich auf $1-{\left(\frac{5}{6}\right)}^{10}\approx \mathrm{83,8}\%.$