Binomialverteilung

Wir betrachten eine Bernoulli-Kette der Länge n und der Erfolgswahrscheinlichkeit p. Die Anzahl der Erfolge ist dann eine Zufallsgröße, die die Werte 0, 1, 2 ... n annehmen kann. Die zugehörige Wahrscheinlichkeitsverteilung wird Binomialverteilung oder auch bernoullische bzw. newtonsche Verteilung genannt.

Ein Zufallsgröße X mit den Werten 0, 1, 2 ... n heißt binomial verteilt mit den Parametern n und p, wenn gilt:

$P\left(X=k\right)=\left(\begin{array}{c}n\\ k\end{array}\right)\cdot p^k\cdot {\left(1-p\right)}^{n-k}(k=0;1\mathrm{...}n)$

Diese Verteilung wird Binomialverteilung mit den Parametern n und p genannt.

Beispiel:
Es wird das 10-malige Werfen einer idealen Münze betrachtet, wobei Wappen als Erfolg und Zahl als Misserfolg gewertet wird.

Mit n = 10 und p = 0,5 erhalten wir für die Anzahl k der Erfolge:

$\begin{array}{l}P\left(X=k\right)=\left(\begin{array}{c}10\\ k\end{array}\right)\cdot {\mathrm{0,5}}^k\cdot {\mathrm{0,5}}^{10-k}\\ =\left(\begin{array}{c}10\\ k\end{array}\right)\cdot {\mathrm{0,5}}^{10}(k=0;1\mathrm{...}10)\end{array}$

Es ergibt sich folgende Wahrscheinlichkeitsverteilung:

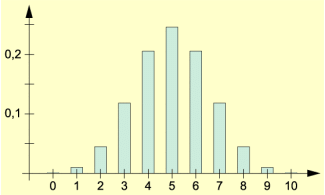
Das zugehörige Diagramm in Bild 1 zeigt den typischen Verlauf einer Binomialverteilung. Bis zu einem bestimmten Wert steigen die Wahrscheinlichkeiten an, dann fallen sie wieder. Für p = 0,5 sind die Diagramme symmetrisch.

Eine Veranschaulichung der Binomialverteilung ist mithilfe des sogenannten Galton-Brett möglich. In vielen Tafelwerken findet man auch Tabellen der Binomialverteilung für bestimmte Parameterwerte von n und p.

Der Erwartungswert einer binomial verteilten Zufallsgröße X berechnet sich wie folgt:

$E\left(X\right)=n\cdot p$

Im Fall des oben betrachten 10-maligen Münzwurfs ergibt sich $E\left(X\right)=10\cdot \mathrm{0,5}=5$.

Für das Beispiel des fünfmaligen Würfelns mit Sechs als Erfolg (s. Beispiel im Thema „Bernoulli-Ketten“) erhielte man
$E\left(X\right)=5\cdot \frac{1}{6}=\frac{5}{6}$.