Kenngrößen der Binomialverteilung
Kenngrößen von Zufallsgrößen dienen deren quantitativer Charakterisierung. Wir betrachten im Folgenden binomialverteilte Zufallsgrößen.
- Eine binomialverteilte Zufallsgröße besitzt den folgenden Erwartungswert :
Diese Aussage kann streng mathematisch bewiesen werden, indem man z.B. die Eigenschaft oder die Rekursionseigenschaft
der Binomialkoeffizienten nutzt.
Grafikfähige Taschenrechner oder auch der Computer bieten überdies die Möglichkeit einer stichprobenartigen Bestätigung der obigen Formel (was nachstehend angedeutet werden soll).
Für berechnet sich der Erwartungswert nach folgender Formel:
Es ist demzufolge nachzuweisen, dass gilt:
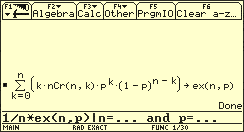
Dies kann stichenprobenartig für beliebige n und p kontrolliert werden. Die folgende Abbildung zeigt z.B. die Berechnung von
Bestätigt wird der Wert 0,456.
![]()
Auch eine interaktive Kontrolle ist möglich.
-
Erwartungswert einer binomialverteilten Zufallsgröße
- Eine binomialverteilte Zufallsgröße besitzt die folgende Streuung :
Auch hier soll die Richtigkeit dieser Formel durch eine stichprobenartige Kontrolle belegt werden.
Für berechnet sich die Streuung nach folgender Formel:
Demzufolge ist nachzuweisen, dass für beliebige n und p gilt:
Die folgende Abbildung bestätigt diese Aussage z.B. für und .
![]()
Auch eine interaktive Kontrolle ist möglich.
-
Streuung einer binomialverteilten Zufallsgröße

Ein Beispiel und drei Lösungsideen
Beispiel: Wie viele nicht geworfene Augenzahlen sind in einer Serie von sechs Würfen mit einem idealen Würfel zu erwarten, dessen Seitenflächen mit den Augenzahlen 1 bis 6 durchnummeriert sind?
Definiert man als Zufallsgröße X die zufällige Anzahl der nicht geworfenen Augenzahlen bei sechs Würfen, so ist der Erwartungswert EX gesucht.
- Lösungsidee 1 (Reales Experiment)
Führt man hinreichend viele derartige Sechs-Wurf-Serien mit einem entsprechenden nicht gezinkten Würfel durch und ermittelt bei jeder Serie die Anzahl der nicht geworfenen Augenzahlen, so ergibt deren arithmetisches Mittel einen Näherungswert für den gesuchten Erwartungswert EX.
- Lösungsidee 2 (Computersimulation)
Mithilfe der Randomfunktion kann eine solche Sechs-Wurf-Serie simuliert werden.
-
Programm zum Ermitteln der zu erwartenden Anzahl nicht gefallener Augenzahlen in einer Sechs-Wurf-SAerie mittels Computersimulation
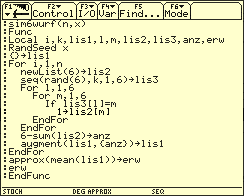
Die folgende Abbildung zeigt das Ergebnis bei Simulationen von 5, 10 und 100 Sechs-Wurf-Serien.
![]()
- Lösungsidee 3 (Theoretischer Ansatz)
Um EX berechnen zu können, muss die Verteilung von X bekannt sein. Da X als „zufällige Anzahl ... bei sechs Würfen“ definiert ist, liegt der Gedanke nahe, X durch eine BERNOULLI-Kette der Länge zu modellieren, d.h. anzusehen (wobei p die Erfolgswahrscheinlichkeit des dazugehörigen BERNOULLI-Experiments ist.)
Aber welches BERNOULLI-Experiment gehört zur Zufallsgröße „zufällige Anzahl der nicht geworfenen Augenzahlen bei sechs Würfen“?
Auf den ersten Blick scheint es nahe liegend zu sein, das einmalige Würfeln in der Sechs-Wurf-Serie als BERNOULLI-Experiment zu wählen. Bei genauerer Betrachtung stößt man aber auf eine Reihe von Widersprüchen.
Zum Beispiel wäre die Wahrscheinlichkeit, beim ersten Wurf eine noch nicht gewürfelte Augenzahl zu würfeln, , beim zweiten Wurf wäre sie aber . Damit wäre aber eine wesentliche Bedingung einer BERNOULLI-Kette – gleiche Erfolgswahrscheinlichkeit p – nicht erfüllt.
Als BERNOULLI-Experiment betrachten wir daher jetzt eine ganze Sechs-Wurf-Serie. Als „Erfolg“ wird bewertet, wenn eine bestimmte, aber beliebige Augenzahl k nicht geworfen wird. Die Erfolgswahrscheinlichkeit p ist dann unabhängig von der konkreten Augenzahl k und zwar .
Realisiert man dieses BERNOULLI-Experiment für jede Augenzahl k genau einmal, so ist die Anzahl aller eingetretenen „Erfolge“ gleich der Anzahl der nicht geworfenen Augenzahlen in einer Wurfserie. Man erhält also ein geeignetes Modell der zu untersuchenden BERNOULLI-Kette, d.h. es ist:
Es sind also etwa 2,009 nicht geworfene Augenzahlen in einer Sechs-Wurf-Serie zu erwarten.

