Rechenregeln für Erwartungswerte

• Satz 1: Ist X eine endliche Zufallsgröße, so gilt für den Erwartungswert der Zufallsgröße $a\cdot X+b$: $E\left(a\cdot X+b\right)=a\cdot EX+b\left(a,b\in ℝ\right)$

Beweis:
Die Zufallsgröße X nehme die Werte $x_i$ mit den Wahrscheinlichkeiten $P\left(X=x_i\right)füri=\mathrm{1,}\mathrm{2,}\mathrm{...},n$ an. Dann gilt:
$\begin{array}{l}E\left(aX+b\right)={\displaystyle \sum _{i=1}^n\left(a{x}_i+b\right)}\cdot P\left(aX+b=a{x}_i+b\right)\\ ={\displaystyle \sum _{i=1}^n\left(a{x}_i+b\right)}\cdot P\left(X=x_i\right)\\ =a\cdot {\displaystyle \sum _{i=1}^n{x}_i\cdot }P\left(X=x_i\right)+b\cdot {\displaystyle \sum _{i=1}^{n}P\left(X=x_i\right)}\\ =a\cdot EX+b\cdot 1=a\cdot EX+bw.z.b.w.\end{array}$

Beispiel 1: Beim einmaligen Werfen eines fairen Tetraeders werde jeweils das um zwei verkleinerte Dreifache der geworfenen Augenzahl notiert.
Welcher Wert ist dann zu erwarten?

Lösungsvariante 1 (nach Satz 1):
Es ist
$X\stackrel{\wedge}{=}\left(\begin{array}{cccc}1& 2& 3& 4\\ \frac{1}{4}& \frac{1}{4}& \frac{1}{4}& \frac{1}{4}\end{array}\right)\Rightarrow EX=\mathrm{2,5}$
und $Y=3\cdot X-2$.

Somit gilt nach Satz 1:
$EY=E\left(3\cdot X-2\right)=3\cdot EX-2=3\cdot \mathrm{2,5}-2=\mathrm{5,5}$

Lösungsvariante 2 (nach Definition):
$\begin{array}{l}Y=3X-2\stackrel{\wedge}{=}\left(\begin{array}{cccc}1& 4& 7& 10\\ \frac{1}{4}& \frac{1}{4}& \frac{1}{4}& \frac{1}{4}\end{array}\right)\\ \Rightarrow EY=1\cdot \frac{1}{4}+4\cdot \frac{1}{4}+7\cdot \frac{1}{4}+10\cdot \frac{1}{4}=\mathrm{5,5}\end{array}$

Lösungsvariante 3 (mittels Simulation):
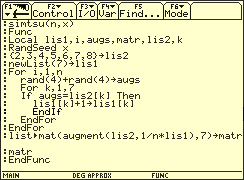
Mithilfe der Randomfunktion eines Taschencomputers wird die Zufallsgröße $Y=a\cdot X+b$ simuliert und n-mal realisiert. Die entsprechenden relativen Häufigkeiten werden als Näherungswerte für die Wahrscheinlichkeiten $P\left(Y=y_i\right)$ verwandt und daraus wird EY berechnet.
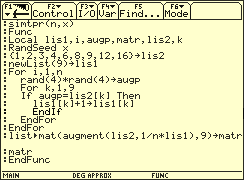
Simulation für $n=200$ ergibt $EY=\mathrm{5,55}$.

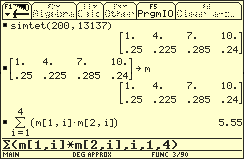
Interaktiv kann die Simulation auch für andere Werte von n durchgeführt werden.

• Satz 2: Für beliebige endliche Zufallsgrößen X und Y gilt: $E\left(X+Y\right)=EX+EY$

Beweis:
Die Zufallsgröße X nehme die Werte $x_i$ mit den Wahrscheinlichkeiten $P\left(X=x_i\right)füri=\mathrm{1,}\mathrm{2,}\mathrm{...},n$ und die Zufallsgröße Y die Werte $y_k$ mit $P\left(Y=y_k\right)fürk=\mathrm{1,}\mathrm{2,}\mathrm{...,}m$ an. Dann gilt:
$\begin{array}{l}E\left(X+Y\right)={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^m\left(x_i+y_k\right)}}\cdot P\left(X=x_{i}undY=y_k\right)\\ ={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^m\left[x_i\cdot P\left(X=x_{i}undY=y_k\right)+y_k\cdot P\left(X=x_{i}undY=y_k\right)\right]}}\\ ={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^m{x}_i\cdot P\left(X=x_{i}undY=y_k\right)+}}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^m{y}_k\cdot P\left(X=x_{i}undY=y_k\right)}}\\ ={\displaystyle \sum _{i=1}^n{x}_i{\displaystyle \sum _{k=1}^{m}P\left(X=x_{i}undY=y_k\right)+}}{\displaystyle \sum _{k=1}^m{y}_k{\displaystyle \sum _{i=1}^{n}P\left(X=x_{i}undY=y_k\right)}}\\ ={\displaystyle \sum _{i=1}^n{x}_i\cdot P\left(X=x_i\right)}+{\displaystyle \sum _{k=1}^m{y}_k\cdot P\left(Y=y_k\right)}=EX+EYw.z.b.w.\end{array}$

Beispiel 2: Beim zweimaligen Werfen eines idealen Tetraeders werde jeweils die Augensumme, d.h. die Summe der beiden geworfenen Augenzahlen, notiert.
Welche Augensumme ist dann zu erwarten?

Lösungsvariante 1 (nach Satz 2):
$\begin{array}{l}X\stackrel{\wedge}{=}\left(\begin{array}{cccc}1& 2& 3& 4\\ \frac{1}{4}& \frac{1}{4}& \frac{1}{4}& \frac{1}{4}\end{array}\right)\Rightarrow EX=\mathrm{2,5}\\ Z=X+X\\ EZ=E\left(X+X\right)=EX+EX=\mathrm{2,5}+\mathrm{2,5}=5\end{array}$

Anmerkung: Für Zufallsgrößen X gilt das aus Zahlenbereichen und Vektorräumen bekannte Gesetz $X+X=2X$ nicht.

Lösungsvariante 2 (nach Definition):
$\begin{array}{l}Z\stackrel{\wedge}{=}\left(\begin{array}{ccccccc}2& 3& 4& 5& 6& 7& 8\\ \frac{1}{16}& \frac{2}{16}& \frac{3}{16}& \frac{4}{16}& \frac{3}{16}& \frac{2}{16}& \frac{1}{16}\end{array}\right)\\ EZ=2\cdot \frac{1}{16}+3\cdot \frac{2}{16}+4\cdot \frac{3}{16}+5\cdot \frac{4}{16}+6\cdot \frac{3}{16}+7\cdot \frac{2}{16}+8\cdot \frac{1}{16}=5\end{array}$

Lösungsvariante 3 (mittels Simulation):
Vorgegangen wird wie in Lösungsvariante 3 des 1. Beispiels.
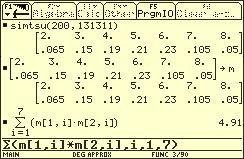
Die Simulation für n = 200 ergibt $EZ=\mathrm{4,91}$.

Interaktiv kann die Simulation auch für andere Werte von n durchgeführt werden.

• Satz 3: Für voneinander stochastisch unabhängige endliche Zufallsgrößen X und Y gilt: $E\left(X\cdot Y\right)=EX\cdot EY$

Beweis:
Die Zufallsgröße X nehme die Werte $x_i$ mit den Wahrscheinlichkeiten $P\left(X=x_i\right)füri=\mathrm{1,}\mathrm{2,}\mathrm{...},n$ und die Zufallsgröße Y die Werte $y_k$ mit $P\left(Y=y_k\right)fürk=\mathrm{1,}\mathrm{2,}\mathrm{...,}m$ an.

Dann gilt (wegen der Unabhängigkeit von X und Y):
$\begin{array}{l}E\left(X\cdot Y\right)={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^m{x}_i\cdot y_k\cdot P\left(X=x_{i}undY=y_k\right)}}\\ ={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^m{x}_i\cdot y_k\cdot P\left(X=x_i\right)}}\cdot P\left(Y=y_k\right)\\ =\left[{\displaystyle \sum _{i=1}^n{x}_i\cdot P\left(X=x_i\right)}\right]\cdot \left[{\displaystyle \sum _{k=1}^m{y}_k\cdot P\left(Y=y_k\right)}\right]\\ =EX\cdot EYw.z.b.w.\end{array}$

Beispiel 3: Beim zweimaligen Werfen eines nichtgezinkten Tetraeders werde jeweils das Augenprodukt, d.h. das Produkt der beiden geworfenen Augenzahlen, notiert.
Welches Augenprodukt ist dann zu erwarten?

Lösungsvariante 1 (nach Satz 3):
Es ist
$\begin{array}{l}X\stackrel{\wedge}{=}\left(\begin{array}{cccc}1& 2& 3& 4\\ \frac{1}{4}& \frac{1}{4}& \frac{1}{4}& \frac{1}{4}\end{array}\right)\Rightarrow EX=\mathrm{2,5}undZ=X\cdot X\\ \end{array}$
(wobei X und X stochastisch unabhängig sind).

Dann gilt:
$EZ=E\left(X\cdot X\right)=EX\cdot EX=\mathrm{2,5}\cdot \mathrm{2,5}=\mathrm{6,25}$

Lösungsvariante 2 (nach Definition):
$\begin{array}{l}Z\stackrel{\wedge}{=}\left(\begin{array}{ccccccccc}1& 2& 3& 4& 6& 8& 9& 12& 16\\ \frac{1}{16}& \frac{2}{16}& \frac{2}{16}& \frac{3}{16}& \frac{2}{16}& \frac{2}{16}& \frac{1}{16}& \frac{2}{16}& \frac{1}{16}\end{array}\right)\\ EZ=1\cdot \frac{1}{16}+2\cdot \frac{2}{16}+3\cdot \frac{2}{16}+4\cdot \frac{3}{16}+6\cdot \frac{1}{16}+8\cdot \frac{2}{16}\\ +9\cdot \frac{1}{16}+12\cdot \frac{2}{16}+16\cdot \frac{4}{16}=\mathrm{6,25}\end{array}$

Lösungsvariante 3 (mittels Simulation):
Vorgegangen wird wieder wie in Lösungsvariante 3 des 1. Beispiels.
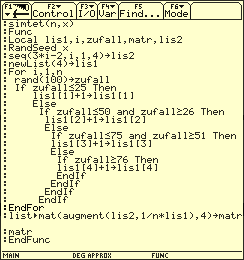
Die Simulation für n = 200 ergibt $EZ=\mathrm{6,18}$.

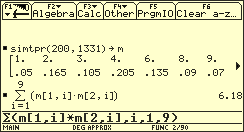
Interaktiv kann die Simulation auch für andere Werte von n durchgeführt werden.