Direkte Proportionalität
Bewegt sich ein Fahrzeug mit gleichbleibender Geschwindigkeit v = 90 km/h (also v = 1,5 km/min) längs eines geradlinigen Weges, so legt es nach den Gesetzen der Physik in der Zeit t die Strecke
(t in Minuten, s in Kilometer) zurück.
Durch die Gleichung wird jedem Wert von t eindeutig ein Wert von s zugeordnet – es handelt sich bei diesem Zusammenhang also um eine Funktion .
Bewegt sich ein Fahrzeug mit gleichbleibender Geschwindigkeit
v = 90 km/h (also v = 1,5 km/min) längs eines geradlinigen Weges, so legt es nach den Gesetzen der Physik in der Zeit t die Strecke
(t in Minuten, s in Kilometer) zurück.
Durch die Gleichung wird jedem Wert von t eindeutig ein Wert von s zugeordnet – es handelt sich bei diesem Zusammenhang also um eine Funktion . Ihr Definitionsbereich ist das betrachtete Zeitintervall (z. B. , gemessen in Minuten), ihr Wertebereich die Menge der zugeordneten Streckenlängen (im Beispiel also , gemessen in Kilometern).
| Zeit t in min | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | 5,5 | 6 |
| Strecke s in km | 0 | 0,75 | 1,5 | 2,25 | 3 | 3,75 | 4,5 | 5,25 | 6 | 6,25 | 7,5 | 8,25 | 9 |
Die Funktion ist in diesem Falle jedoch durch spezifische Merkmale gekennzeichnet:
- Je länger die Fahrzeit ist, desto größer ist der zurückgelegte Weg, wobei die Fahrtzeiten und die Streckenlängen sich im gleichen Verhältnis vergrößern: Verdoppelt (verdreifacht) sich die Fahrtzeit, so verdoppelt (verdreifacht) sich auch die Länge zurückgelegten Strecke.
- Die Quotienten aus den Streckenlängen und den zugehörigen Zeiten (wie auch umgekehrt die Quotienten aus den Zeiten und den zugehörigen Streckenlängen) sind gleich (wobei wir hier den „Start-Quotienten“ herausnehmen):
In Worten: Je Minute legt das Auto jeweils 1,5 km zurück.
Oder:
In Worten: Für ein Kilometer benötigt das Auto etwa 0,67 min. - Man kann alle Streckengrößen erhalten, indem man die jeweilige Zeit mit dem Faktor 1,5 km/min multipliziert.
Oder:
Man kann die für jede Strecke benötigte Zeit erhalten, indem man die jeweilige Streckenlänge mit dem Faktor 0,67 min/km multipliziert. - In einem Koordinatensystem liegen alle Punkte, die den Wertepaaren aus einer Zeitgröße und der zugehörigen Streckenlänge entsprechen, auf ein und derselben Geraden durch den Koordinatenursprung.
Oder:
In einem Koordinatensystem liegen alle Punkte, die den Wertepaaren aus einer Streckenlänge und der hierfür benötigten Zeit entsprechen, auf ein und derselben Geraden durch den Koordinatenursprung.
Diese vier Eigenschaften sind jede für sich Ausdruck des spezifischen Merkmals der in dem obigen Beispiel beschriebenen Funktion: Es handelt sich hierbei um eine direkte Proportionalität.
-
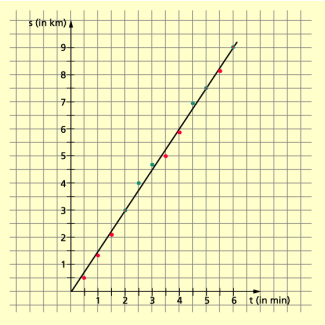
Weg-Zeit-Diagramm
Einen Zuordnung heißt direkte Proportionalität, wenn zwei veränderliche Größen x und y immer den gleichen Quotienten k haben, wenn also gilt:
Man schreibt auch y ~ x (gesprochen: y ist proportional zu x).
Verallgemeinert man die oben getroffenen Feststellungen, so lässt sich eine direkte Proportionalität zweier Größen durch folgende – untereinander gleichwertige – Merkmale kennzeichnen:
- Vergrößerungen (Verkleinerungen) der beiden Größen erfolgen jeweils im gleichen Verhältnis. Also: Wird die eine Größe verdoppelt (verdreifacht, halbiert ...), so verdoppelt (verdreifacht, halbiert ...) sich auch die andere Größe.
- Alle Quotienten einander zugeordneter Werte sind gleich
(Quotientengleichheit): - Wenn man die Werte der einen Größe mit ein und demselben Faktor (Proportionalitätfaktor k) multipliziert, so erhält man die jeweils zugeordneten Werte der anderen Größe. Für einander entsprechende Werte x und y gilt also:
- Die den Wertepaaren der beiden Größen entsprechenden Punkte mit den Koordinaten liegen in einem Koordinatensystem auf ein und derselben Geraden durch den Koordinatenursprung.

