Falten
Die Mittelsenkrechten, Seitenhalbierenden und Winkelhalbierenden eines aus Papier ausgeschnittenen beliebigen Dreiecks lassen sich durch Falten erzeugen.
Die Schnittpunkte der Mittelsenkrechten, der Winkelhalbierenden, der Seitenhalbierenden und der Höhen eines aus Papier ausgeschnittenen beliebigen Dreiecks lassen sich durch Falten erzeugen.
-
Dreieck mit Mittelsenkrechten, Seitenhalbierenden, Winkelhalbierenden, Höhen und der eulerschen Geraden
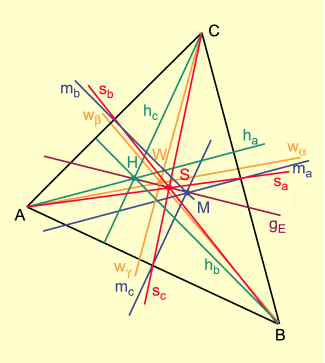
Mittelsenkrechte
Man faltet die Eckpunkte paarweise aufeinander, die entstehende Faltlinie, die senkrecht zur Seite ist, halbiert diese auch. Faltet man alle drei Mittelsenkrechten, so erhält man auch ihren Schnittpunkt.
Winkelhalbierende
Man faltet zwei benachbarte Seiten so aufeinander, dass die Faltlinie durch den gemeinsamen Eckpunkt verläuft. Alle drei Winkelhalbierenden schneiden sich in einem Punkt.
Seitenhalbierende
Durch Faltlinien, die jeweils den Seitenmittelpunkt und den gegenüberliegendem Eckpunkt verbinden, lässt sich auch der Schwerpunkt bestimmen.
Man kann die Richtigkeit und Genauigkeit seiner Faltung dadurch überprüfen, das der Schnittpunkt der Seitenhalbierenden und der Mittelsenkrechten auf einer Geraden liegen. Dies kann auch durch eine Faltlinie erfolgen, die die eulersche Gerade des Dreiecks ist.
Höhen
Die Höhen sind die Lote von einem Eckpunkt auf die jeweils gegenüberliegende Seite. Beim Falten müssen die Teilstrecken der jeweiligen Seite sich decken und die Faltlinie muss durch den Eckpunkt gehen. Faltet man alle drei Höhen, so erhält man den Höhenschnittpunkt. Beim spitzwinkligen Dreieck befindet sich der Höhenschnittpunkt im Inneren des Dreiecks, beim stumpfwinkligen Dreieck befindet er sich außerhalb des Dreiecks. Dieser Fall lässt sich nicht durch Falten darstellen.
Im rechtwinkligen Dreieck sind die beiden Katheten auch Höhen. Der Höhenschnittpunkt ist mit dem Scheitelpunkt des rechten Winkels identisch.

