Euler, Mathematische Beiträge

LEONHARD EULERs besondere Liebe galt der Zahlentheorie. „Er rechnete, wie andere atmen“, sagte ein Zeitgenosse über ihn. Es wird glaubhaft berichtet, dass EULER in einer Zeit, da er nachts keinen Schlaf fand, die Potenzen der natürlichen Zahlen bis 20 im Kopf bis zu $n^6$ berechnete und die Ergebnisse dauerhaft behielt.
Bei der Suche nach Termen, die nur Primzahlen liefern, hatte
FERMAT 1640 den Term $2^{2^n}+1$ gefunden, der für die Zahlen 1, 2, 3 und 4 tatsächlich auf Primzahlen führt. Für n = 5 erhält man die Zahl $4294967297$, die man auch für eine Primzahl hielt. EULER fand heraus, dass sich diese Zahl als Produkt $641\cdot 6700417$schreiben lässt, wobei er sich wahrscheinlich einiger von ihm gefundener Hilfssätze bediente. Er selbst nannte in diesem Zusammenhang den Term $n^2+n+41$, bei dem für die natürlichen Zahlen bis 39 tatsächlich jeweils Primzahlen herauskommen. Andere Theoreme FERMATs konnte EULER dagegen beweisen, z. B. den folgenden Satz:

Jede Primzahl der Form 4n + 1 lässt sich als Summe zweier einander teilerfremder Quadrate schreiben
(etwa $29=5^2+2^2;37=6^2+1^2;73=8^2+3^2$).

Er bewies auch den sogenannten „Kleinen Fermat“:

Für alle Primzahlen p und alle natürlichen Zahlen a ist $a^p-a$stets durch p teilbar
(für p = 3 und a = 2 bzw. a =5 gilt z. B. $3{|2}^3-2=6$und $5{|5}^3-5=120$).

Ganz andersartig ist das Problem, mit dessen Lösung er sogar eine neue mathematische Teildisziplin, die Topologie begründete. Ausgangspunkt dafür war das „Königsberger Brückenproblem“. In dieser Stadt gab es eine Insel, die von zwei Flussarmen umgeben ist, über die sieben Brücken führen. Niemand hatte einen Weg gefunden, bei dem man jede dieser Brücken genau einmal überschreitet. EULER wies nach, dass das auch nicht möglich ist, wenn es mehr als zwei Gebiete gibt, für die die Anzahl der Zugangsbrücken ungerade ist.

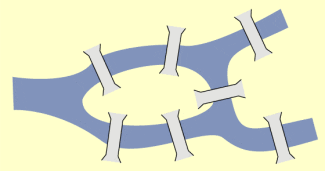
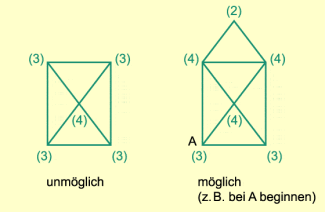
Aus gleichen Überlegungen ergibt sich, dass man eine Figur nicht in einem Zuge zeichnen kann, wenn es in ihr mehr als zwei Knotenpunkte gibt bei denen eine ungerade Zahl von Linien hin- bzw. wegführt.

Mit ähnlichen Überlegungen bewies EULER den nach ihm benannten Polyedersatz :

Für alle konvexen Polyeder gilt:
$e+f=k+\mathrm{2,}$
wobei e die Anzahl der Ecken, f die der Flächen und k die der Kanten bedeutet.

Seinen Namen trägt auch die eulersche Gerade . Für alle Dreiecke gilt, dass der Schnittpunkt der Höhen, der Schnittpunkt der Mittelsenkrechten und der der Seitenhalbierenden auf einer (nämlich dieser) Geraden liegen.

1744 erschien EULERs Lehrbuch über Variationsrechnung, das sich mit Problemen der Berechnung von Extremwerten (Maximum und Minimum) befasste. 1748 veröffentlichte er die erste analytische Geometrie der Kegelschnitte in Lehrbuchform, worin sich auch Entwicklungen von Reihen für $\sin x,\cos xund{e}^x$ finden.

EULER hat mehr als 900 Abhandlungen verfasst, mehr als die Hälfte davon während seiner Blindheit.
Dank des großen Ansehens, das er genoss, haben viele Begriffe und Symbole, die er in seinen Werken einführte oder übernahm, durch ihn Eingang in die Mathematik gefunden und werden heute noch von uns benutzt. Dazu gehören beispielsweise:

• a, b, c für die Seiten und $\alpha ,\beta ,\gamma$ für die Winkel eines Dreiecks
• das Zeichen $\pi$ für die Kreiszahl
• sin, cos und tan als Streckenverhältnisse
• die Zahl e als Grenzwert von ${\left(1+\frac{1}{n}\right)}^n$, Basis der natürlichen Logarithmen
• das Zeichen $\Delta x$ für den Differenzenquotienten
• das Summenzeichen ${\displaystyle \sum }$
• das Symbol i für $\sqrt{-1}$
• das Symbol $f\left(x\right)$ für Funktionen, für die er auch eine Definition angab

CARL FRIEDRICH GAUSS schrieb über EULER: Von keinem anderen Mathematiker neuerer oder älterer Zeit kann man eine solche fast unbegreifliche Schnelligkeit in den schwierigsten Arbeiten bei einer solchen unerschöpflichen Fruchtbarkeit an neuen Ideen und Hilfsmitteln rühmen. Alle Teile der Mathematik bearbeitete er, und die meisten erhielten unter seinen Händen eine ganz neue Gestalt.