Ganze Zahlen, Rechnen

Beim Rechnen mit ganzen Zahlen kann man die Verfahren des Rechnens mit natürlichen Zahlen anwenden; es sind dann immer nur gesonderte Überlegungen zur Ermittlung des Vorzeichens im Ergebnis nötig.

Addition

Die Addition ist im Bereich der ganzen Zahlen eindeutig und stets ausführbar.

Zwei ganze Zahlen mit gleichen Vorzeichen werden wie folgt addiert:

1. Man bildet die Beträge und addiert sie.
2. Man gibt der Summe das Vorzeichen der Ausgangswerte.

Zwei ganze Zahlen mit unterschiedlichen Vorzeichen werden wie folgt addiert:

1. Man bildet die Beträge und subtrahiert den kleineren vom
   größeren Betrag.
2. Man gibt der Summe das Vorzeichen, das die Zahl mit dem
   größeren Betrag hat.

$\begin{array}{l}\left(+3\right)+\left(+4\right)=3+4=7\\ \left(-117\right)+\left(117\right)=0\end{array}$

Subtraktion

Die Subtraktion ganzer Zahlen wird auf die Addition ganzer Zahlen zurückgeführt.
Da zu jeder ganzen Zahl eine entgegengesetzte Zahl existiert und die Addition im Bereich der ganzen Zahlen stets ausführbar ist, ist auch die Subtraktion stets ausführbar.
Eine ganze Zahl wird subtrahiert, indem man die zu ihr entgegengesetzte Zahl addiert: $a-b=a+\left(-b\right)$

$\begin{array}{l}5-3=5+\left(-3\right)=2\\ 5-8=5+\left(-8\right)=-3\\ 5-\left(-3\right)=5+3=8\\ \left(-5\right)-3=\left(-5\right)+\left(-3\right)=-8\end{array}$

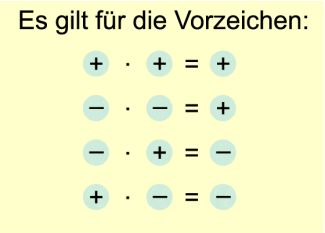
Multiplikation

Zwei ganze Zahlen werden multipliziert, indem man ihre Beträge multipliziert und das Vorzeichen des Produkts gesondert bestimmt. Das Produkt ist

• positiv, wenn beide Faktoren gleiche Vorzeichen haben,
• negativ, wenn beide Faktoren unterschiedliche Vorzeichen haben. $\begin{array}{l}3\cdot 7=213\cdot \left(-7\right)=-21\\ \left(-3\right)\cdot 7=-21\left(-3\right)\cdot \left(-7\right)=21\end{array}$

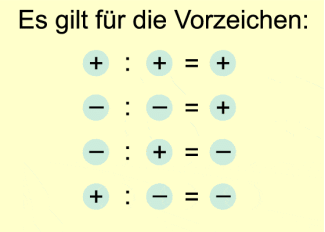
Division

Eine ganze Zahl a wird durch eine ganze Zahl b dividiert, indem man den Betrag von a durch den Betrag von b dividiert und das Vorzeichen des Quotienten gesondert bestimmt.
Der Quotient ist

positiv, wenn der Dividend a und der Divisor b das gleiche
Vorzeichen haben,

negativ, wenn der Dividend a und der Divisor b unterschiedliche Vorzeichen haben.