Geschichte der Zahl Null

Ein Zeichen für die Null wurde wohl schon vor über fünftausend Jahren benutzt. Die Mesopotamier gebrauchten in ihren Verträgen die Null als Begriff für „nichts“.
Vor 300 v. Chr. benutzten auch babylonische Gelehrte für das „Nichts“ ein Zeichen, dieses bestand aus zwei schräg gestellten Pfeilen. Wurde dieses Zeichen in eine Zeichenfolge für Ziffern eingefügt, so bedeutete dies, dass an dieser Stelle „nichts“ sei.

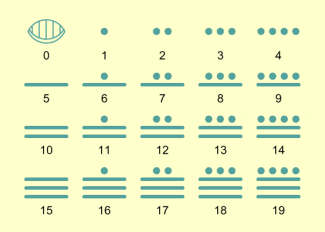
Aus etwa der gleichen Zeit stammen Aufzeichnungen der Maya, aus denen hervorgeht, dass sie auf der Basis der Zahl 20 (Finger und Zehen) ein Zahlsystem entwickelt hatten, das auch ein Zeichen für die Zahl Null enthielt. So begann beispielsweise jeder Monat mit dem nullten Tag.

Die Mayas benutzten für ihre Zahlen ein Positionssystem. Das bedeutet: Der Wert einer Ziffer innerhalb einer Zahl hängt davon ab, an welcher Position (Stelle) die Zahl steht. In der Zahl 452 beispielsweise steht die erste Ziffer für „hundert“, die zweite für „zehn“ und die dritte für „eins“. Mit einer begrenzten Zahl von Grundziffern ließen sich so alle Zahlen darstellen.
Die Griechen verwendeten ein Additionssystem in Form von Buchstaben, in dem die Null nicht vorkam. So stand das H für Hekaton, für 100. Um die Zahl 87 zu schreiben, brauchten die Griechen zwei Zeichen, das P für 80 und das Z für 7, die addiert wurden.

Die römischen Zahlzeichen bestanden aus vier Grundzeichen und drei Hilfszeichen, deren Werte addiert bzw. subtrahiert wurden. Um „komplizierte“ Zahlen darstellen zu können, wurden diese Zeichen hintereinandergeschrieben. Beispielweise entspricht die Zeichenfolge DCCCLXXXVIII der Zahl 888.

Da sowohl Griechen als auch Römer auf dem Abakus (einem Rechenbrett) rechneten, brauchten sie keine Null(en). Die entsprechenden Stellen (Spalten für Einer, Zehner, Hunderter, Tausender) blieben einfach leer. So besitzt die Zahl 3055 keine Hunderter, also blieb die Hunderterspalte auf dem Abakus frei.
Besonders deutlich wurde das Dilemma mit der Null bei der Entwicklung des Kalenders, denn die ersten stellten die Römer auf. Da diese keine Null kannten, ließ die Kirche bei der Einführung des julianischen Kalenders auf das Jahr 1 vor Christus das Jahr 1 nach Christus folgen. Ein Jahr Null gab es nicht (demzufolge hat das 21. Jahrhundert eigentlich erst am 1. Januar 2001 begonnen).

Die Zahl Null wurde erstmals in Indien verwandt, nicht als Platzhalter wie bei den Mayas, sondern als vollwertige Zahl. Mit ihr wurde (nach heute noch gültigen Regeln) addiert, subtrahiert und multipliziert.
Um 711 übernahmen die Araber die indischen Zahlzeichen. Der persische Mathematiker MUHAMMAD IBN MUSA AL-CHWARIZMI (787 bis 850, Bild 3) stellt in seiner Schrift „Die Zahlen der Inder“ die Zahl Null als Kreis vor.
Bis hinein ins Mittelalter war die Zahl Null in Europa weitgehend unbekannt, sofern sie nicht durch Handelsreisende, die z. B. aus Indien davon Kenntnis erhielten, mitgebracht wurde. Vielen Menschen war das „runde Ding“ ein Werk des Teufels und somit unheimlich.
Versuche (etwa von AURILAC, einem Mönch und späteren Papst), die arabischen Zahlen in Europa einzuführen, scheiterten hauptsächlich am Widerstand der Kirche.

Insbesondere der italienische Mathematiker LEONARDO FIBONACCI VON PISA (etwa 1180 bis etwa 1250) leistete einen großen Betrag zum Siegeszug der Null. Er stellte in seinem Buch „Liber abaci“ die Vorteile dieser Zahlen an konkreten Aufgaben aus der Kaufmannslehre dar. Auf der Suche nach Rechenregeln und Rechenverfahren begegnete auch den Rechenmeister n der Renaissance, wie ADAM RIES (1492 bis 1559), ständig das Problem der Null (denn diese Zahl wurde gebraucht, um mithilfe eines Stellenwertsystems rechnen zu können). Ihren Bemühungen ist es zu verdanken, dass die Null schrittweise in den Rechenstuben Einzug hielt.
Mit der Verwendung der arabischen Schrift brachte die Null sogar den eigenen Namen mit, denn Null heißt auf arabisch „sifr“. Daraus entstand das Wort „Ziffer“ (man geht davon aus, dass auch das Wort „zero“ davon abgeleitet wurde).
Aus der Bezeichnung für „Nichts“ wurde also der mathematische Begriff Null (lat. nulla figura svw. keine Zahl).

Welche Bedeutung die Null über die Mathematik hinaus hat, soll die folgende Begebenheit deutlich machen: Während einer Übungsfahrt des US-amerikanischen Kreuzers „Yorktown“ wurde 1977 ein neues Computerprogramm getestet. Urplötzlich schalteten sich alle Aggregate ab, das Schiff war schlagartig manövrierunfähig. Alle Systeme, einschließlich des neuen Programms, wurden überprüft. Dabei stellte sich heraus, dass eine einzige Null Ursache für den Totalausfall war. Die Programmierer hatten an einer Stelle die Division durch Null programmiert. Der Rechner hatte nun versucht, dieser Aufforderung nachzukommen bis seine Kapazität erschöpft war und er sich abschaltete ...
Der amerikanische Wissenschaftsjournalist CHARLES SEIFE schreibt in seinem Buch „Zwilling der Unendlichkeit. Eine Biographie der Zahl Null “: Die Null lässt uns das Unbeschreibliche und das Unendliche erahnen. Und deshalb wird sie ja so gefürchtet und gehasst - und geächtet.