Intervallhalbierungsverfahren
Zur näherungsweisen Bestimmung einer reellen Zahl nutzt man eine Intervallschachtelung. Das Intervallhalbierungsverfahren ist eine spezielle Intervallschachtelung, bei der die Intervalllänge in jedem Schritt halbiert wird. Diese Verfahren ist zwar einfach durchzuführen, aber es erfordert viele Rechenschritte bis man die gewünschte Genauigkeit erzielt hat.
Zur näherungsweisen Bestimmung einer reellen Zahl nutzt man eine Intervallschachtelung. Das Intervallhalbierungsverfahren ist eine spezielle Intervallschachtelung, bei der die Intervalllänge in jedem Schritt halbiert wird. Diese Verfahren ist zwar einfach durchzuführen, aber es erfordert viele Rechenschritte bis man die gewünschte Genauigkeit erzielt hat.
Beispiel:
Bestimmen von![]() mit dem Halbierungsverfahren
mit dem Halbierungsverfahren
Das Ergebnis 3 ist bekannt auch ohne Intervallschachtelung, somit ist jeder Schritt nachvollziehbar.
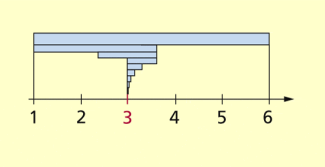
Begonnen wird mit dem Intervall [1; 6]. Es wird zerlegt in die halben Intervalle [1; 3,5] und [3,5; 6]. Die zweite Hälfte wird weggelassen, da bereits 3,5² = 12,25 zu groß ist. Man behält das Intervall
[1; 3,5], weil 1² ≤ 9 ≤ 3,5², d. h. ![]()
![]() [1; 3,5]. Mit dem halbierten Intervall [2,25; 3,5] wird genauso verfahren usw. (Bild 1).
[1; 3,5]. Mit dem halbierten Intervall [2,25; 3,5] wird genauso verfahren usw. (Bild 1).
| I1 = [1; 3,5] | I6 = [2,95312; 3,03125] | ||
| I2 = [2,25; 3,5] | I7 = [2,99218; 3,03125] | ||
| I3= [2,875; 3,5] | I8 = [2,99218; 3,01171] | ||
| I4 = [2,875; 3,03125] | I9= [2,99218; 3,00195] | ||
| I5 = [2,875; 3,03125] | I10= [2,99707; 3,00195] |
Das Halbierungsverfahren liefert eine unendliche Folge von Intervallen. Im obigen Beispiel wurde nur bis zum Intervall I10 auf maximal sechs Ziffern gerechnet, aber prinzipiell könnte das Verfahren fortgesetzt werden. Das Intervallhalbierungsverfahren liefert eine Intervallschachtelung, die genau eine Zahl definiert. Unterschiedliche Intervallschachtelungen können für dieselbe Zahl genutzt werden.
Beispiel:
Bestimmen von ![]() mit dem Halbierungsverfahren
mit dem Halbierungsverfahren
| I0 = [1; 2] | Als Startintervall I0 sei I0 = [1; 2] gewählt. | I0 = [1; 2] | |||
| I1 = [; ] | Denn es muss | I1 = [1; 1,5] | |||
| I2 = [; ] | weil 1² = 1 < 2 und 2² = 4 > 2 ist. | I2 = [1,25; 1,50] | |||
| I3 = [; ] | Die Mitte 1,5 teilt I0 in zwei Hälften. | I3 = [1,375; 1,500] | |||
| ... | Als Intervall I1 wird [1; 1,5] genommen, | ... | |||
| I20 = [;] | denn 1,5² (= 2,25) ist größer als 2. | I20 = [1,414213; 1,414214] |
Auf diese Weise ergibt sich eine Intervallschachtelung für ![]() , deren erste Intervalle links in Bruchform und rechts in Dezimalschreibweise zu sehen sind.
, deren erste Intervalle links in Bruchform und rechts in Dezimalschreibweise zu sehen sind.
Das Halbierungsverfahren ist universell einsetzbar. Ohne die vielseitige Einsetzbarkeit zu verlieren, kann man das Verfahren dem Dezimalsystem dadurch anpassen, dass jedes Intervall in zehn gleiche Teile zerlegt wird. Allerdings muss man häufiger prüfen, welches der Teilintervalle die gesuchte Zahl enthält. Dann aber liefert jeder Teilschritt eine Dezimalstelle mehr.
-
Veranschaulichung des Intervallhalbierungsverfahrens