Sekantennäherungsverfahren

Die regula falsi ist ein Näherungsverfahren zum Bestimmen der Lösungen von Gleichungen, bei denen die Anwendung exakter Verfahren zur Berechnung nicht existieren oder in ihrer Handhabung zu aufwendig sind.
Das gilt z. B. für das Bestimmen der Lösungen von Gleichungen dritten oder höheren Grades mit einer Unbekannten, für Wurzelgleichungen, Exponentialgleichungen, Logarithmengleichungen und trigonometrische Gleichungen. Aber auch die Berechnung krummlinig begrenzter Flächen oder krummflächig begrenzter Körper erfordert meist den Einsatz von Näherungsverfahren.

Ein Grundgedanke der Näherungsverfahren zum Bestimmen der Lösungen von Gleichungen besteht darin, die Gleichung in eine Funktionsgleichung umzuwandeln, sodass die Variable der Gleichung als Veränderliche der Funktion erscheint. Gesucht wird dann die Nullstelle dieser Funktion. Statt der Gleichung p(x) = 0 wird die Funktion f(x) = p(x) betrachtet. Dieses „Suchen“ bedeutet, dass man eine z. B. durch Probieren mit speziellen Werten oder durch Schätzen gefundene Näherungslösung schrittweise verbessert oder ein Intervall, in dem die Lösung liegt, systematisch verkleinert.

Ein seit dem Mittelalter benutztes Verfahren zur Nullstellenbestimmung ist als regula falsi (Regel des falschen Wertes) oder Sekantennäherungsverfahren bekannt.

Um die Lösungen der Gleichung p(x) = 0 zu bestimmen, wird die Funktion f(x) = p(x) betrachtet. In dem Intervall $\left[x_0;x_1\right]$ existiert dann mindestens eine Nullstelle, wenn die Funktion in dem Intervall stetig ist und an den Intervallenden unterschiedliche Vorzeichen hat. Die Kurvenpunkte an den Enden des Intervalls werden durch eine Gerade (die Sekante) verbunden und der Schnittpunkt dieser Geraden mit der x-Achse wird als eine Verbesserung des Intervalls betrachtet. Das Ausgangsintervall wird dadurch in zwei kleinere Intervalle zerlegt. Mit dem Teilintervall, in dem jetzt die Nullstelle liegt, wird dann die Iteration (Näherung) fortgesetzt.

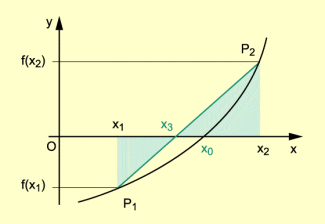
Der Schnittpunkt der Sekante mit der x-Achse wird bestimmt, indem man den Strahlensatz anwendet. Der berechnete Wert wird als verbesserte Lösung betrachtet (Bild 2).

Aus der Strahlensatzfigur des Bildes folgt:
         $\frac{{\text{x}}_{\text{2}}-{\text{x}}_{\text{0}}}{\text{f}\left({\text{x}}_{\text{0}}\right)}=-\frac{{\text{x}}_{\text{1}}-{\text{x}}_{\text{2}}}{\text{f}\left({\text{x}}_{\text{1}}\right)}$,
wobei das Minuszeichen den Vorzeichenwechsel von f(x) korrigiert.

Die Abszisse von x ergibt sich aus der Umformung der letzten Gleichung:
${\text{x}}_{\text{2}}={\text{x}}_{\text{0}}-\text{f}\left({\text{x}}_{\text{0}}\right)\frac{{\text{x}}_{\text{1}}-{\text{x}}_{\text{0}}}{\text{f}\left({\text{x}}_{\text{1}}\right)-\text{f}\left({\text{x}}_{\text{0}}\right)}$

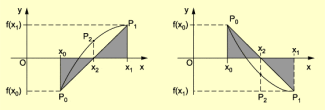
Dieses Vorgehen wird mit dem verkleinerten Intervall wiederholt, wobei derjenige der Punkte $P_0$ und $P_1$ durch den Punkt $P_2\left(x_2;f\left(x_2\right)\right)$ ersetzt wird, dessen Ordinate das Vorzeichen von $f\left(x_2\right)$ hat. Je nachdem, welcher der Punkte $P_0$ oder $P_1$ ersetzt wird, übernimmt das errechnete $x_2$ die Funktion von ${\text{x}}_{\text{0}}$ oder ${\text{x}}_{\text{1}}$. Die völlig gleichartige Rechnung liefert dann einen neuen Wert $x_2$. Man beendet die Iteration, wenn die vorgegebene Genauigkeit erreicht ist.