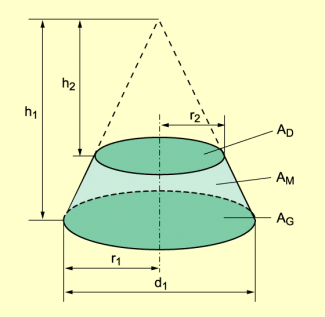
Kegelstumpf
Wird ein gerader Kreiskegel von einer parallel zu Grundfläche verlaufenden Ebene geschnitten, so entsteht ein gerader Kegelstumpf. Die parallelen Flächen und sind zueinander ähnliche Kreise.
Wird ein gerader Kreiskegel von einer parallel zu Grundfläche verlaufenden Ebene geschnitten, so entsteht ein gerader Kreiskegelstumpf (kurz: Kegelstumpf) und ein Ergänzungskegel. Die parallelen Flächen und sind zueinander ähnliche Kreise. Für die Grundfläche und die Deckfläche gilt:
ist dabei die Höhe des vollständigen Kegels, die Höhe des Ergänzungskegels. Des Weiteren gilt für die Länge der Seitenkante s des Kegelstumpfes:
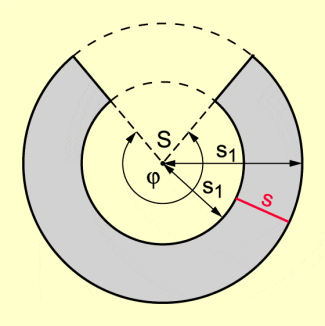
Wird die Mantelfläche eines geraden Kreiskegels in einer Ebene abgewickelt, so entsteht der Ausschnitt eines Kreisrings. Der Flächeninhalt dieses Kreisringausschnitts entspricht dem Flächeninhalt des Mantels des Kegelstumpfes.
Für den Oberflächeninhalt des geraden Kegelstumpfes gilt dann:
Das Volumen des Kegelstumpfes ist die Differenz der Volumina des Kreiskegels und des Ergänzungskegels. Für das Volumen des Kegelstumpfes gilt dann:
-
Schrägbild eines Kreiskegelstumpfes
-
Abwicklung des Mantels eines geraden Kreiskegelstumpfes