Pyramide

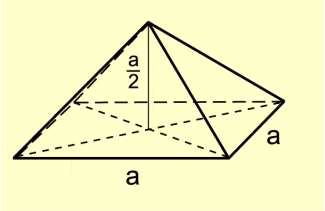
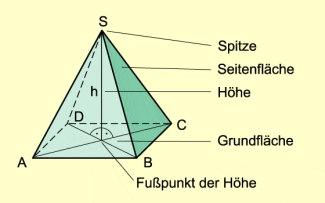
Ein Körper heißt Pyramide (Bild 1), wenn er von einem Dreieck, Viereck, Fünfeck usw. als Grundfläche und von Dreiecken als Seitenflächen begrenzt wird, die einen Punkt S gemeinsam haben. Der Punkt S heißt Spitze der Pyramide. Der Abstand der Spitze der Pyramide von der Grundfläche heißt Höhe der Pyramide. Der Fußpunkt der Höhe ist der Fußpunkt des Lotes von der Spitze in die Grundfläche. Die Kanten der Grundfläche nennt man Grundkanten, die Kanten der Seitenfläche heißen Seitenkanten.
Pyramiden können nach der Anzahl ihrer Seitenflächen unterschieden werden.

Eine dreiseitige Pyramide, deren Kanten alle gleich lang sind, heißt Tetraeder.

Eine Pyramide mit einem Quadrat bzw. Rechteck als Grundfläche heißt quadratische bzw. rechteckige Pyramide.
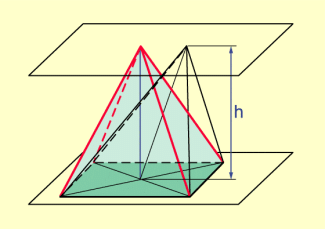
Die Spitze einer Pyramide kann bei gleicher Höhe verschiedene Lagen haben (Bild 2).
Wenn die Grundfläche einen Umkreis hat und der Fußpunkt der Höhe zugleich der Mittelpunkt des Umkreises der Grundfläche ist, sind alle Seitenkanten der Pyramide gleich lang und die Pyramide ist gerade.
Die Seitenflächen sind in diesem Fall gleichschenklige Dreiecke.

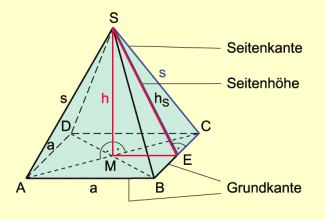
Bei Pyramiden muss man zwischen der Körperhöhe h und den Höhen $h_s$ der Seitenflächen unterscheiden.
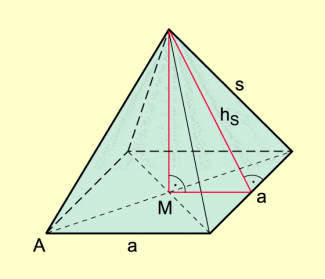
Für eine quadratische Pyramide (Bild 3) ergeben sich durch Anwendung des Satzes des Pythagoras auf die Dreiecke EMS und CES folgende Beziehungen:
$h^2+{\left(\frac{a}{2}\right)}^2=h_s{}^2{\text{ h}}_{\text{s}}{}^2+{\left(\frac{a}{2}\right)}^2=s^2$
Daraus ergibt sich:
$h^2+\frac{a^2}{2}=s^2$

Die Oberfläche $A_O$ einer Pyramide setzt sich aus ihrer Grundfläche $A_G$und ihrer Mantelfläche $A_M$ zusammen. Der Mantel wird von den Seitendreiecken der Pyramide gebildet.
Der Oberflächeninhalt einer Pyramide ist gleich der Summe aus den Inhalten der Grundfläche und der Mantelfläche:
$A_O=A_G+A_M$
Für eine quadratischen Pyramide (Bild 4) mit der Grundkantenlänge a und der Seitenflächenhöhe $h{}_s$ gilt:
$\begin{array}{l}{A}_M=4\cdot \frac{1}{2}\cdot a\cdot h_s=2\cdot a\cdot h_s\\ A_O=a^2+2\cdot a\cdot h_s=a\cdot \left(a+2h_s\right)\end{array}$

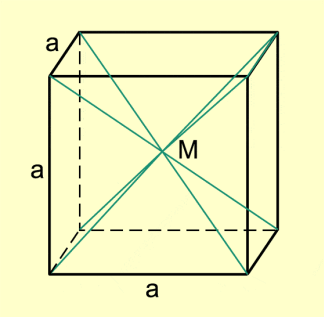
Um das Volumen einer quadratischen Pyramide zu bestimmen, kann man einen Würfel in sechs gleich große quadratische Pyramiden mit der gemeinsamen Spitze im Würfelmittelpunkt zerlegen (Bild 5). Die sechs Pyramiden haben alle die Grundkante a und die Höhe $h=\frac{1}{2}a$. Da das Würfelvolumen $a^3$beträgt, ergibt sich für das Volumen jeder der Pyramiden:

$V=\frac{1}{6}{a}^3$

Für die Grundfläche der Pyramide gilt (Bild 6):
$A_G=a^2$
Für ihre Höhe gilt:
$h=\frac{1}{2}a$
Daraus ergibt sich:
$V=\frac{1}{3}\cdot a^2\cdot \frac{1}{2}\cdot a=\frac{1}{3}{A}_G\cdot h$
Diese Beziehung gilt nicht nur für die spezielle Pyramide, sondern für alle quadratischen Pyramiden und sogar für jede Pyramide mit beliebiger Grundfläche und beliebiger Höhe.
Das Volumen einer Pyramide ist gleich einem Drittel des Produktes aus der Grundfläche und der Höhe:
$V=\frac{1}{3}{A}_G\cdot h$